Школьный этап Сириус по Математике для 2-ой группы 15 октября 2025 г.
Вопросы и ответы 6 класс
Задание 1. Из 27 кубиков размером 1×1×1 сложили куб 3×3×3. Он состоит из 11 красных и 16 синих кубиков.
Какая наименьшая площадь поверхности куба 3×3×3 может быть красной?
Какая наибольшая площадь поверхности куба 3×3×3может быть красной?
Задание 2. Даны два квадрата с целыми сторонами a и b (a<b).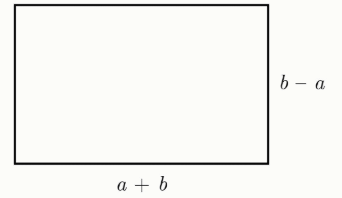
Площадь изображённого прямоугольника равна 47.
Найдите a.
Найдите b.
Задание 3. Назовём горизонталь, вертикаль или одну из двух главных диагоналей квадрата рядом. В квадрате 3×3 расставили числа так, что для любого его ряда верно, что число, расположенное в его середине, вдвое меньше суммы крайних чисел этого ряда. Из квадрата стёрли некоторые числа. Восстановите их.
Задание 4. На плоскости проведены 32 прямые, причём каждая параллельна ровно трём другим и никакие три прямые не пересекаются в одной точке. Сколько точек пересечения у этих прямых?
Задание 5. По кругу стоят 60 чередующихся стульев: чёрных и белых. На стулья сели представители двух племён: рыцари и лжецы. Рыцари всегда говорят правду, лжецы всегда лгут. Каждый сидящий на белом стуле заявил, что среди двух человек, следующих за ним по часовой стрелке, есть рыцарь. Каждый сидящий на чёрном стуле заявил, что среди двух человек, следующих за ним по часовой стрелке, нет рыцаря. Сколько рыцарей могло сидеть за столом? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 6. В каждом столбце, в каждой строке и в каждой выделенной фигуре таблицы должно быть по одной букве A, B, C, D, E. Таблицу заполнили частично.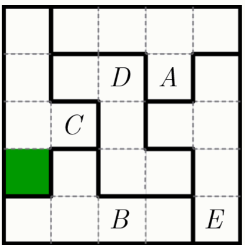
Какая буква расположена в отмеченной клетке?
Задание 7. Роботы‑рекультиваторы ликвидируют последствия разлива радиоактивного вещества, снимая верхний слой почвы с участка. Вся загрязнённая почва может быть убрана одним роботом за 42 часа. Ангар с первым роботом располагается в 1 км от участка, со вторым в 2 км и т. д. Все роботы выехали из ангаров одновременно и начинали удаление почвы, как только достигали участка. Когда последний робот добрался до участка, оказалось, что загрязнённую почву только что полностью убрали. Известно, что первый робот убрал в шесть раз больше предпоследнего. Производительность и скорость передвижения всех роботов одинакова.
Сколько часов снимал почву первый робот?
Сколько часов первый робот ехал до поля?
Задание 8. В государстве 28 городов располагаются на территории областей так, что любые два города из одной области соединены дорогой и никакие два города из разных областей дорогой не соединены. Оказалось, что ответственность за состояние дорог можно распределить между двумя региональными министерствами следующим образом: не найдётся таких трёх городов A, B, C из одной области, чтобы дороги AB , BC и CA обслуживались бы одним министерством. Какое наибольшее число дорог может быть в этом государстве?
Олимпиада «Сириус» ответы, вопросы по Математике 6 класс, школьный этапа Всероссийской олимпиады 2 группа от 15 октября 2025 года. Официальный вариант с вопросами на логику, головоломки.




 Задания
Задания