Факультатив по математике, 4 класс. Решение задач на чётностьВнеурочное занятие по математике для 4 класса. Тема: Задачи на четность и свойства четности
Цель: повторить понятие четности, научить применять свойства четности чисел при решении некоторых видов задач.
Примечание. При решении задач на эту тему потребуется вспомнить следующие свойства четных и нечетных чисел:
— сумма двух четных чисел — четное число;
— сумма двух нечетных чисел — четное число;
— сумма четного и нечетного чисел — нечетное число;
— произведение двух чисел, хотя бы одно из которых четное, будет четным.
Ход занятия
Решение задач.
Задача 1. Можно ли заплатить без сдачи 20 копеек семью монетами?
Решение.
Да, можно: 10 + 5 + 1 + 1 + 1 + 1 + 1= 20.
Задача 2. Можно ли заплатить без сдачи 20 копеек семью монетами по 1 к. и по 5 к.?
Решение.
Нет, так как сумма семи нечетных чисел не может быть четным числом.
Задача 3. Можно ли заплатить без сдачи 25 копеек восемью монетами по 1 к. и по 5 к.?
Решение.
Нет, нельзя, так как сумма восьми нечетных чисел будет четной.
Задача 4. Вася записал на листе несколько нечетных чисел. Петя их не видел, но утверждает, что по их числу легко определить, четная или нечетная у них сумма. Прав ли Петя?
Решение.
Петя прав, так как сумма нечетного числа нечетных чисел будет нечетной, а сумма четного числа нечетных чисел будет четной.
Задача 5. Некто пообещал дать 99 конфет тому, кто сумеет их разделить между 4 детьми так, чтобы каждому досталось нечетное число конфет. Почему этот приз до сих пор никому не удалось получить?
Решение.
Потому что сумма 4 нечетных чисел должна быть четной, а 99 — нечетное число.
Задача 6. Саша купил в магазине 20 тетрадей, 2 альбома для рисования, авторучку за 4 р., несколько карандашей по 1 р. 20 к. и несколько ластиков по 8 к. Ему сказали, что надо уплатить в кассу 38 р. 65 к. Саша попросил пересчитать стоимость покупки. Как он догадался, что была допущена ошибка?
Решение.
Так как для каждого из видов купленных предметов или количество предметов или цена предмета являются четным числом, то сумма всей покупки должна быть четной, а 38 руб. 65 коп. — нечетное число, значит, допущена ошибка.
Задача 7. Коля уверяет, что знает 4 целых числа, произведение и сумма которых — нечетные числа. Не ошибается ли он?
Решение.
Ошибается, так как если все 4 числа нечетные, то их сумма обязательно будет четной. А если хотя бы одно число будет четным, то их произведение будет четным.
Задача 8. Записано четыре числа: 0, 0, 0, 1. За один ход разрешается прибавить 1 к любым двум из этих чисел. Можно ли за несколько ходов получить 4 одинаковых числа?
Решение.
Нет. Сумма четырех данных чисел нечетная, а сумма четырех равных чисел, которые надо получить, — четная. Из первой суммы нельзя получить вторую, прибавляя несколько раз по 2.
Задача 9. Карлсон предложил Малышу следующую игру. На столе лежат две кучки спичек — 7 и 8 спичек. Первый игрок делит одну из кучек на 2 кучки, затем второй делит одну из двух кучек на две кучки и т. д. Проигрывает тот, кто не сможет сделать очередного хода. Карлсон начинает. Кто выиграет в этой игре? Зависит ли результат от того, кто как играет? Или важно лишь то, кто ходит первым?
Решение.
При любой тактике игры Малыш проиграет, так как получить из 2 кучек 15 можно только за 13 ходов, то есть последний ход всегда будет за Карлсоном.
Задача 10. Имеется 9 листов бумаги. Некоторые из них разорвали на 3 или на 5 частей. Некоторые из образовавшихся частей опять разорвали на 3 или на 5 частей, и так несколько раз. Можно ли после нескольких таких операций получить 100 частей?
Решение.
Разрывая лист на 3 или на 5 частей, мы к данному количеству частей добавляем 2 или 4 части соответственно, но, прибавляя к нечетному числу 9 четные числа сколько угодно раз, мы не сможем получить четное число 100.
Задача 11. Во время сбора грибов мальчик 5 раз переходил полотно одной и той же железной дороги.
По одну или по разные стороны от полотна железной дороги находятся мальчик и его дом?
Решение.
Мальчик переходит железную дорогу нечетное число раз (5), то есть он окажется по другую сторону дороги от своего дома.
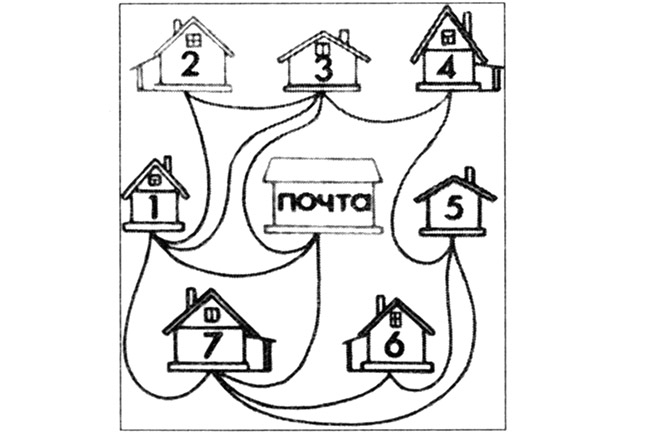
Задача 12. Почтальон Печкин разнес почту во все дома деревни, после чего зашел к дяде Федору.
На рис. 1 показаны все тропинки, по которым проходил Печкин, причем, как оказалось, ни по одной из них он не проходил дважды. Каков мог быть маршрут почтальона Печкина?
В каком доме живет дядя Федор?
Решение.
Тропинки образуют сеть с двумя «нечетными» узлами — у почты и у дома № 5. Начало маршрута на почте, а конец — у дома № 5. Значит, там и живет дядя Федор.
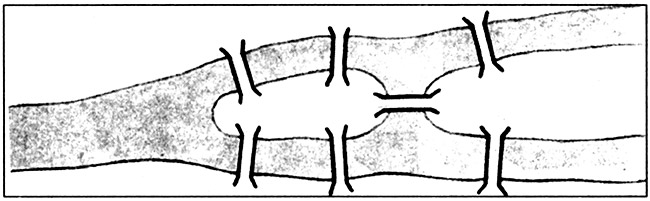
Задача 13 (задача Леонарда Эйлера). Можно ли поочередно обойти все 7 мостов Кенигсберга (ныне Калининград), соединяющих районы этого города с островами на реке Преголя, проходя по каждому мосту только один раз? (Рис. 2.)
Домашнее задание:
Задача 1. При каких значениях переменной значение выражения делится на 2:
758 + х; 1643 • у; p — 916 • 835; 5000 • b?
Задача 2. Реши уравнение:
(50х — 85) : 9 + 48 = 83
Решение.
(50х-85) : 9 = 35
50x 85 = 315
50х = 400
х = 8
Ответ: 8.
222 — (560 : у + 43) = 99
Решение.
(560 : у + 43) = 123
560 :у = 80
у = 560 : 80
у = 7
Ответ: 7.