Сценарий интеллектуальной игры «Морской бой» по математике для старшеклассников (10 класс)
«Морской бой» — излюбленная игра и младших, и старших школьников.
Главная цель — «потопить» корабли противника путем прямого попадания в корабль.
Игровое поле— квадрат, состоящий из 10 строк, обозначенных числами от 1 до 10, и 10 столбиков, обозначенных буквами от А до К. Координаты цели определяются именем столбца и строки.
В эту игру могут играть 2-3 команды. Игровое поле — одно для всех команд. Это квадрат больших размеров, который находится на видном месте, все 100 его клеток закрыты квадратиками из картона или бумаги. На игровом поле размешены «корабли»: четырехпалубный, трехпалубные, двухпалубные и однопалубные. Количество кораблей и их размеры можно менять по своему усмотрению.
Все клетки «кораблей» закрашены. Клетки, касающиеся бортов корабля, обозначены буквами, соответствующими разделу математики или темы. «А» — алгебра; «С» — задачи на смекалку; «Ч» — все о числах; «К» — комбинаторика; «Г» — геометрия; «Л» — логические задачи; «И» — из истории математики; «М» — о математиках. (Последние две темы связаны между собой.)
Остальные клетки пустые. Участникам необходимо «овладеть» всеми кораблями. По очереди команды делают выстрелы (указывают координаты на игровом поле). Ведущий открывает указанный квадратик. Если под ним окажется одна из палуб корабля, то команде сразу начисляется 1 очко и дается право на следующий выстрел. Если произошло попадание в букву, то это значит, что рядом находится борт одного из кораблей. Команде задается соответствующий вопрос. На обдумывание ответа— 30 с. Если ответ правильный, команда также получает 1 очко и право на следующий выстрел. Игра завершается после того, как участники «потопят» все корабли. Побеждает команда, набравшая наибольшее количество очков.

Перечень вопросов
Вопросы из области алгебры:
1) Д1. У мальчика сестер столько же, сколько и братьев, а у девочки братьев в три раза больше, чем сестер. Сколько в семье братьев и сколько сестер? (3 брата и 2 сестры.)
2) Е1. В 12 часов дня часовая и минутная стрелки совпадают. Через сколько минут после этого они снова совпадут? (Через 65 5/11 мин.)
3) Ж1. Вычислите:
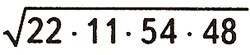
Ответ: 792.
4) З2. Некто продает свою лошадь по числу подковных гвоздей, которых у нее 16. За первый гвоздь он просит 1 руб., за второй — 2 руб., за третий — 4 руб., за четвертый — 8 руб. и за каждый следующий вдвое больше, чем за предыдущий. Во сколько он ценит свою лошадь?
Решение:
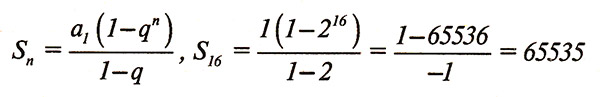
Ответ: 65535 руб.
5) ЖЗ. За одно качание воздушный насос откачивает из резервуара 0,1 воздуха. Сколько процентов воздуха останется после 5 качаний? (59%.)
6) ЕЗ. Куплены тетради по 7 руб. и по 4 руб. за тетрадь, всего на сумму 53 руб. Сколько куплено тех и других тетрадей? (7 тетрадей по 7 руб. и 1 тетрадь по 4 руб.)
7) ДЗ. Кирпич имеет массу 1,5 кг и еще полкирпича. Какова масса кирпича? (3 кг.)
8) Г2. Что больше:
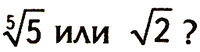
Решение:
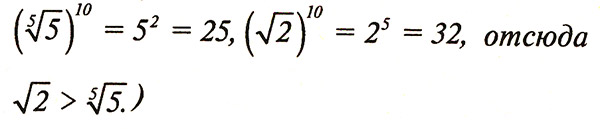
Задачи на смекалку:
9) Б1. В комнате четыре угла. В каждом углу сидит кошка. На хвосте у каждой кошки по одной кошке. Сколько всего кошек в комнате? (4 кошки.)
10) В2. Число 666 увеличить в полтора раза, не производя никаких арифметических действий? (Перевернуть, будет 999.)
11) ВЗ. Может ли дробь, в которой числитель меньше знаменателя, быть равной дроби, в которой числитель больше знаменателя? (Может, например, -3/6 = 5/-10)
12) Б4. Сколько ударов в сутки делают часы с боем? (156 ударов.)
13) АЗ. К Айболиту пришли на прием животные: все, кроме двух, собаки; все, кроме двух, кошки; все, кроме двух, зайцы. Сколько всего животных? (3.)
14) А2. Президент кондитерской компании спрашивает: «Чье предложение принять, если первый дилер предлагает за продукцию 216 тыс. руб., а второй — ((22)2)2 тыс. руб.? (Первое, так как 216 > 28.)
Вопросы из области геометрии:
15) А4. Можно ли вычислить длину дуги, если известно только число градусов, содержащихся в этой дуге? (Нельзя, нужно знать еще длину радиуса.)
16) А6. Аист бумаги надо разрезать на 8 частей, ограниченных отрезками. Сколько разрезов нужно сделать? (7разрезов.)
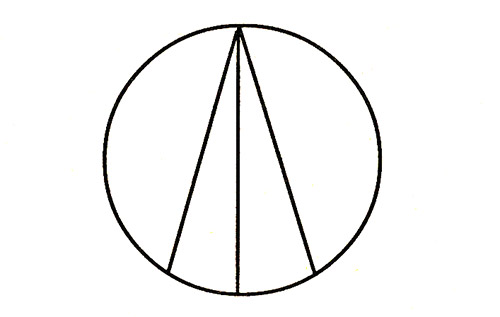
17) Б5. Из одной точки окружности проведены 3 хорды. Сколько получилось сегментов? (6 сегментов.)
Вопросы из области чисел и числовых множеств:
18) Г4. Что больше: 1020 или 2010? (1020> 2010, так как 1010 • 1010 > 1010 • 210.)
19) Д4. Тремя тройками, не употребляя знаков действий, записать возможно большее число. (З33.)
20) Е4. Полтрети — число 100. Что это за число? (600.)
21) Ж4. Сколько сейчас времени, если до конца суток осталось столько, что уже протекло от начала суток? (13 часов 20 минут.)
22) 35. Какое натуральное число в 7 раз больше цифры его единиц? (35.)
23) Ж6. Какое наибольшее число можно записать при помощи четырех единиц? (1111)
24) Е6. Какая цифра будет последней в записи результата 95399999? (7, так как 9534 • 24989 • 9533 а 33 оканчивается на 7.)
25) Д6. Как изменится дробь, если числитель ее увеличить на знаменатель? (Увеличится на 1.)
26) Г6. Арбуз на ¾ кг тяжелее ¾ этого арбуза. Сколько весит арбуз? (3 кг.)
27) В5. Половина — треть числа. Какое это число? (1,5.)
Логические задачи:
28) И6. Разложите термины в логической последовательности: а) геометрический образ; б) квадрат; в) плоская фигура; г) выпуклый многоугольник. (а), в), г), б).)
29) К7. В доме 6 этажей. Во сколько раз путь по лестнице на 6 этаж длиннее, чем на 3, если лестницы имеют одинаковое количество ступенек? (В 2 раза.)
30) К8. 5 землекопов за 5 ч выкопают 5 м канавы. Сколько землекопов за 100 ч выкопают 100 м канавы? (5.)
31) И9. Какой знак нужно поставить между числами 5 и 6, чтобы получилось число больше 5, но меньше 6? (Запятую, получится 5,6.)
32) 38. Встретились три мальчика: Белов, Чернов, Рыжов.
— Вы только посмотрите, — воскликнул Белов, — у нас у всех разные волосы, и их цвет не совпадает с фамилией.
— Ты прав, — ответил ему черноволосый мальчик.
Определите цвет волос каждого. (Белов — рыжий, Чернов — белый, Рыжов — черный.)
33) 37. На столе лежат в ряд квадрат, круг и треугольник (в таком порядке). Одна из фигур красного цвета, другая — желтого, третья — синего. Квадрат не красный, с одной стороны от синей фигуры лежит желтая, а с другой — красная. Определите цвет каждой фигуры. (Квадрат — желтый, круг — синий, треугольник — красный.)
Задачи на комбинаторику:
34) З4. Пять друзей, встретившись, обменялись рукопожатиями. Сколько всего было сделано рукопожатий? (10 рукопожатий)
35) ИЗ. Из семи человек нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать? (35 способами)
36) И5. Сколькими способами могут быть расставлены 8 участниц финального забега на восьми беговых дорожках? (40320 способами, так как Р8 = 8!.)
37) К4. Делится ли число 9! на 90? (Да, так как 90 = = 2 • 5 • 9, а в числе 9! есть числа 2, 5 и 9.)
Вопросы из области истории математики:
38) А8. Кого из великих математиков называют победителем простых чисел? (П. Л. Чебышева.)
39) Б7. Какую аксиому Н. И. Лобачевский положил в основу своей геометрии вместо пятого постулата Евклида? (Через точку, взятую вне прямой на плоскости, можно провести более одной прямой, не пересекающей данную.)
40) Б9. Чью теорему называют «теоремой невесты»? (Теорему Пифагора.)
41) Б7. Кто был создателем первой вычислительной машины? (Б. Паскаль.)
42) В9. Кто автор знаменитого бинома? (И. Ньютон.)
43) Г7. Какому математику поставлен в столице Норвегии памятник, где юноша переступает через двух чудовищ. Математики шутят, что эти чудовища изображают уравнения 5-й степени и эллиптические функции, покоренные юношей. (Нильсу Генрику Абелю.)
44) Г9. Какой математический термин обозначался Radix или R, и что означает запись R212? (Корень из 12)
45) А8. Кого называют математиком из Сиракуз? (Архимеда.)
Вопросы из биографии математиков:
46) Д9. Место рождения русского математика Н. И. Лобачевского. (Нижний Новгород.)
47) Е8. Какую драму написала С. В. Ковалевская? («Борьба за счастье», которая ставилась в Москве в 1894 г.)
48) Е10. Кого из математиков, кроме Лобачевского, можно отнести к творцам неевклидовой геометрии? (Венгерского математика Я. Бояи.)
49) Ж8. Величайший математик XVIII в., родившийся в Швейцарии, считавший Россию второй родиной. С помощью его «изобретения» мы легко решаем логические задачи. (Леонард Эйлер.)
50) Ж10. Ученый-геометр, внесший свой вклад в развитие математики ещё задолго до Евклида, уроженец города Милета, расположенного на берегу Эгейского моря. (Фалес.)
51) 39. Французский ученый, который изобрел метод координат. (Р. Декарт.)




 Математическая игра «Морской бой», 10 класс
Математическая игра «Морской бой», 10 класс