Математические задачи для школьников с решением. Тема: Чётность
Многие задачи легко решаются, если заметить, что некоторая величина имеет определённую чётность. Из этого следует, что ситуации, в которых эта величина имеет другую чётность, невозможны. Иногда надо эту величину сконструировать, например, рассмотреть чётность суммы или произведения, разбить объекты на пары, заметить чередование состояний, раскрасить объекты в 2 цвета. Чётность в играх — возможность сохранить чётность некоторой величины при своём ходе.
Задача 1.
Кузнечик прыгал вдоль прямой и вернулся в исходную точку (длина его прыжка равна 1 м). Доказать, что он сделал чётное число прыжков.
Решение:
Так как кузнечик вернулся в исходную точку, то количество прыжков вправо равно количеству прыжков влево, то есть общее количество прыжков чётное.
Задача 2.
Можно ли в таблицу 5х5записать все числа 1, 2, 3, …, 24, 25 так, чтобы в каждой строке сумма некоторых из записанных в ней чисел равна сумме остальных чисел этой строки?
Решение:
Предположим, что числа в таблицу записаны так, как это требуется в условии. Тогда сумма чисел в каждой строке — чётная. Значит, должна быть чётной и сумма всех чисел в таблице, но она равна: 1 + 2 +… + 24 + 25 = 25 • 12 + 13 = 325, то есть нечётная, получаем противоречие. Значит, требуемого размещения чисел в таблице не существует.
Задача 3.
На доске написаны в строку 2005 целых чисел. Доказать, что одно из них можно стереть, и сумма оставшихся чисел будет чётной. Верно ли это утверждение для 2006 чисел?
Решение:
Если количество нечётных чисел нечётное, то можно стереть любое из них. Если же количество нечётных чисел чётное, то на доске есть хотя бы одно чётное число (всего чисел — 2005). Его и стираем. Если на доске написаны 2006 нечётных чисел, то сумма их чётная и при стирании любого из них сумма оставшихся чисел нечётная.
Задача 4.
— У нас в классе 35 человек. И можешь себе представить, каждый дружит ровно с 11 одноклассниками…
— Не может этого быть, — сразу ответил своему приятелю Витя Иванов, победитель математической олимпиады. Почему он так решил?
Решение: Витя Иванов мог рассуждать так:
— Докажу от противного. Принесу в класс много длинных верёвок. Попрошу каждых двух друзей взять в руки по концу верёвки, соединяющей их. А всего в классе 35 х 11 = 385 концов. Но у верёвки 2 конца, и общее число концов тоже должно быть чётным. Получается противоречие.
Задача 5.
На доске написаны числа 0, 1,0, 0. За один шаг разрешается прибавлять единицу к любым двум из них. Можно ли, повторяя эту операцию, добиться, чтобы все числа стали равными?
Решение:
За один шаг сумма всех написанных чисел увеличивается на 2. Вначале сумма равна 1, поэтому она всегда будет оставаться нечётной. А сумма четырёх одинаковых чисел, очевидно, чётная. Поэтому добиться, чтобы все числа стали равными, невозможно.
Задача 6.
На листке напечатано число 20. 33 ученика передают листок друг другу, и каждый прибавляет к числу или отнимает от него 1 (как хочет). Может ли получиться число 10?
Решение:
Когда очередной ученик прибавляет к числу 1 или отнимает от него 1, чётность этого числа изменяется (чётное число превращается в нечётное, а нечётное — в чётное). У нас было число 20, то есть чётное. Значит, первый ученик превратит его в нечётное, второй — снова в чётное, третий — в нечётное, четвёртый — в чётное, …, тридцать третий — снова в нечётное; но 10 — чётное число, значит, 10 получиться не может.
Задача 7.
100 фишек стоят в ряд. Любые две фишки, расположенные через одну, можно менять местами. Удастся ли расположить фишки в обратном порядке?
Решение:
Переставляя фишки, легко увидеть, что фишка, стоящая на нечётном месте, переходит только на нечётное место. Значит, фишка, стоящая на 1-м месте, не сможет занять последнее сотое (чётное) место.
Задача 8.
Можно ли выбрать 5 чисел из таблицы, сумма которых равна 20?
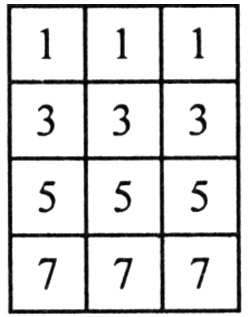
Решение:
Сумма любых пяти нечётных чисел есть число нечётное, а именно такие числа даны в таблице.
Ответ: нет.
Задача 9.
Володя написал на доске 1 * 2 * 3 *… * 9 = 21, поставив вместо каждой звёздочки либо «+», либо « — ». Саша изменил некоторые знаки на противоположные, а в результате вместо 21 написал 20. Докажите, что один из мальчиков ошибся.
Решение:
На доске 5 нечётных чисел, значит, сумма или разность нечётная. Тогда 20 получиться не может. Саша ошибся.
Задача 10.
На доске выписаны числа 1, 2, 3, …, 101. Стирают два произвольных числа и записывают разность стёртых чисел. Повторяют эту операцию 100 раз и в результате получают число р. Докажите, что р отлично от нуля.
Решение:
Для любых двух чисел сумма и разность имеют одинаковую чётность. В качестве инварианта можно взять чётность суммы записанных на доске чисел. 1 + 2 + 3 + … + 101 = (1 + 100) • 50 = 101 = 5050 = 101 = 5151 — нечётное число. Значит, при указанной операции число р — нечётное, а значит, оно не равно нулю.
Задача 11.
Кузнечик прыгает по прямой: первый прыжок — на 1 см, второй — на 2 см и т. д. Может ли он после 25-го прыжка вернуться в точку, с которой начал прыгать?
Решение:
Чтобы кузнечику после 25-го прыжка оказаться в начальной точке, необходимо преодолеть длину, равную чётному числу, но это невозможно, так как 1 + 2 + 3 + … + 13 + … + 25 = (1 + 25) · 12 + 13 — нечётное число.
Задача 12.
Градостроители города Альфа хотят спланировать сеть улиц так, чтобы каждая из 37 улиц была напрямую соединена ровно с 5-ю другими. Удастся ли им это?
Решение:
Предположим, что это возможно. Если 37 умножить на 5, то получим общее количество улиц, при этом каждая улица сосчитана дважды. Но 37 • 5 — нечётное число.
Ответ: нет.
Задача 13.
Даны шесть чисел: 1, 2, 3, 4, 5, 6. Разрешается к любым двум числам прибавлять 1. Можно ли все шесть чисел сделать равными?
Решение:
Сумма данных чисел равна 21. При прибавлении к ним двух единиц каждый раз получаем нечётное число. С другой стороны, сумма шести равных чисел равна чётному числу.
Ответ: нельзя.
Задача 14.
На столе стоят 10 стаканов. Из них 9 стоят правильно, а один перевёрнут вверх дном. Разрешается одновременно переворачивать любые 4 стакана. Можно ли, повторяя эту операцию несколько раз, поставить все стаканы правильно?
Решение:
Одну операцию переворачивания четырёх стаканов можно истолковать как две операции переворачивания двух стаканов. Если переворачивать два правильно стоящих стакана или два неправильно стоящих стакана, то чётность числа правильно стоящих стакана не изменится. А если переворачивать правильно стоящий и неправильно стоящий стаканы, то число правильно стоящих и неправильно стоящих стаканов вообще не изменится. Значит, количество неправильно стоящих стаканов — всегда нечётное число.
Отсюда ответ: нельзя.
Задача 15.
Шахматный конь начинает свой маршрут из левого нижнего угла доски, а кончает его в правом верхнем углу. Может ли конь при этом побывать на всех полях доски в точности по одному разу?
Решение:
При каждом ходе конь меняет цвет поля. Так как начальное и конечное поля одного цвета, то конь сделает чётное число ходов. Но это противоречит тому, что надо сделать коню 63 хода, чтобы побывать на каждом поле.
Ответ: не может.
Задача 16.
На волшебной сосне растут 10 бананов и 9 апельсинов. Если сорвать два одинаковых фрукта, то на сосне тут же вырастет один банан, а если сорвать два разных, то вырастет один апельсин. Срывать фрукты по одному нельзя. Можно ли сорвать фрукты с сосны так, чтобы на сосне остался один банан?
Решение:
Апельсинов всё время остаётся нечётное число, а чтобы последним остался банан, необходимо, чтобы апельсинов перед последним срыванием было чётное число — два или ноль.
Ответ: нельзя.
Задача 17.
В конференции принимали участие 19 учёных. После конференции каждый из них отправил 4 или 2 письма другим учёным; бывшим на конференции. Может ли так случиться, что каждый из них получит по 3 письма?
Решение:
Общее число полученных писем должно равняться числу отправленных писем, которое является чётным.
Ответ: не может.
Задача 18.
Можно ли расставить в клетках квадрата 4×4 натуральные числа таким образом, чтобы любая сумма всех чисел любой строки и любое произведение всех чисел любого столбца были нечётными?
Решение: чтобы произведение чисел столбца было нечётным, нужно, чтобы в каждом столбце стояли только нечётные числа. Но тогда в каждой строке также стоят нечётные числа; следовательно, сумма чисел в каждой строке будет чётной.
Ответ: нельзя.
Задача 19.
За круглым столом сидят 2001 представитель четырёх племён: люди, гномы, эльфы и гоблины. Известно, что люди никогда не сидят рядом с гоблинами, а эльфы никогда не сидят рядом с гномами. Докажите, что какие-то два представителя одного племени сидят рядом.
Решение:
Пусть это не так. Удалим мысленно всех людей и всех гоблинов. Тогда по условию задачи между любыми двумя оставшимися стоит ровно один стул, то есть общее число стульев чётное, что противоречит условию.
Задача 20.
Даны 6 чисел: 11, 22, 33, 44, 55, 66. Разрешается к любым двум числам прибавить 1. Можно ли за несколько таких операций все числа сделать равными?
Решение:
Общая сумма всех 6 чисел изначально нечётная и остаётся нечётной при каждой операции. Если бы все числа стали равными, их сумма была бы чётным числом.
Ответ: нельзя.
Задача 21.
На чудо-яблоне растут бананы и ананасы. За один раз разрешается сорвать с неё 2 плода. Если сорвать 2 банана или 2 ананаса, то вырастет ещё один ананас. Если сорвать один банан и один ананас, то вырастет один банан. Какой плод — оставшийся, если известно, сколько бананов и ананасов росло вначале?
Решение:
Чётность числа бананов не меняется, поэтому если число бананов было чётным, то оставшийся плод — ананас, если число бананов было нечётным, то оставшийся плод — банан.
Задача 22.
На классной доске написаны числа: 2, 3, …, 1975. Разрешается стереть любые два числа, записав вместо них их разность. Доказать, что многократным повторением такой операции нельзя добиться того, чтобы на доске остался один нуль.
Решение: Сумма исходных чисел 2 + 3 + 4 + … + 1973 + 1974 + 1975 = (2 + 1975)•1974/2 = 1977 • 977 — нечётное число.
Если стёрли 2 чётных числа, записав вместо них разность, то разность — чётное число, оно не влияет на чётность суммы чисел. Если стёрли два нечётных числа и заменили их разностью, то разность — чётное число, оно тоже не влияет на чётность суммы чисел. Разность чётного и нечётного чисел — нечётное число — тоже не влияет на чётность суммы написанных чисел. То есть указанная операция не меняет чётность суммы написанных чисел. Сумма исходных чисел нечётная. Значит, последнее оставшееся число — нечётное (не нуль).
Задача 23.
Можно ли натуральные числа от 1 до 21 включительно разбить на несколько групп так, чтобы в каждой группе одно из чисел равнялось сумме всех остальных чисел?
Решение:
Общая сумма всех чисел 1+2 + 3 + … + 19 + 20 + 21=(1 + 21) · 10 + 11= 231 — нечётное число. Если бы было возможно, что одно из чисел в группе равнялось сумме остальных, то сумма всех чисел в группе была бы чётной, а тогда сумма всех чисел от 1 до 21 была бы чётной. Но эта сумма нечётная.
Ответ: требуемое разбиение невозможно.
Задача 24.
Конь начал двигаться с клетки а1 на шахматной доске. Может ли он через 2001 ход вернуться обратно?
Решение:
Каждым своим ходом конь переходит на клетку другого цвета. Следовательно, чтобы вернуться на исходную клетку, ему надо сделать чётное число ходов, а число 2001 — нечётное.
Ответ: нет.
Задача 25.
Можно ли расставить в клетках квадрата 4×4 натуральные числа таким образом, чтобы сумма чисел, стоящих в каждой строке, и произведения чисел, стоящих в каждом столбце, были нечётными?
Решение:
Чтобы произведение чисел в каждом столбце было нечётным, надо, чтобы в каждом столбце стояли только нечётные числа. Но тогда в каждой строке также стоят нечётные числа, а тогда сумма четырёх нечётных чисел будет чётной.
Ответ: нельзя.
Задача 26.
На доске записаны 1993 нуля, 1994 единицы, 1995 двоек. Разрешается стереть любые 2 цифры и записать вместо них третью: вместо 0 и 1 — двойку, вместо 0 и 2 — единицу, вместо 1 и 2 — нуль. После многократного выполнения этой операции на доске осталась 1 цифра. Какая?
Решение:
При замене двух цифр одной цифрой сумма всех имеющихся цифр либо увеличивается на 1, либо уменьшается на 1, либо уменьшается на 3, то есть в любом случае меняет свою чётность. В самом начальном положении сумма всех цифр 1994 • 1 + 1995 • 2 + 1993 • 0 = 5984 — чётная. Всего цифр: 1993 + 1994 + 1995 = — = 5982. Одна цифра останется после 5981 замены, таким образом, последняя цифра — нечётная, то есть 1.
Ответ: 1.
Задача 27.
На столе стоят 16 стаканов. Из них 15 стаканов стоят правильно, а один перевёрнут донышком вверх. Разрешается одновременно переворачивать любые 4 стакана. Можно ли, повторяя эту операцию, поставить все стаканы правильно?
Решение:
Посмотрим, как изменяется количество правильно стоящих стаканов при каждой операции.
Очевидно, это зависит от того, сколько из переворачиваемых стаканов стоят правильно, а сколько — вверх дном, а именно:
— если все 4 переворачиваемых стакана стоят правильно, то количество правильно стоящих стаканов уменьшится на 4;
— если из 4 стаканов правильно стоят 3, то это количество уменьшится на 2;
— если 2, то количество не изменится;
— если 1, то увеличится на 2;
— если все переворачиваемые стаканы стояли вверх дном, то количество правильно стоящих стаканов увеличится на 4.
В любом случае количество правильно стоящих стаканов либо остаётся прежним, либо изменяется на чётное число. Поскольку сначала таких стаканов было 15, то в любой момент их будет нечётное количество. Поэтому добиться, чтобы 16 стаканов стояли правильно, нельзя.
Ответ: нельзя.




 Олимпиадные задачи на тему «Чётность» с ответами, 5 класс
Олимпиадные задачи на тему «Чётность» с ответами, 5 класс