Сценарий мероприятия по математике для учащихся 8 класса «Детективы из нашего восьмого»
На сцену выходят ведущие. Ими могут быть ученики старших классов либо учителя математики. В последнем случае диалоги ведущих немного видоизменяются. Команды участников игры готовятся заранее. В их составе по 7 человек от каждого восьмого класса. Так как в процессе игры игроки выбывают, то этот процесс регулируется учителем, чтобы до конца игры дошли обе команды, причем в проигрывающей команде не должно остаться меньше двух игроков. Если проигрывает одна и та же команда, некоторые игры на выбывание можно пропускать.
Ведущий 1. Скажи, знаешь ли ты хоть одну профессию, в которой не пригодились бы знания математики?
Ведущий 2. Я — нет, а ты?
Ведущий 1. А я вот думал-думал и решил, что, пожалуй, в таких популярных нынче профессиях, как юрист, милиционер, следователь, и без математики вполне можно справиться.
Ведущий 2. Напрасно ты так думаешь. Ведь ни один следователь не смог бы раскрывать запутанные дела, если бы у него не было развито логическое мышление, если бы он не был наблюдательным, внимательным, не имел бы хорошую память, а как раз эти качества лучше всего развивает математика.
Ведущий 1. Ну, если с этой точки зрения посмотреть, тогда, конечно. Ты меня убедил.
Ведущий 2. А как думаешь, есть ли в нашем зале такие школьники, у которых эти качества уже хорошо развиты?
Ведущий 1. Думаю, есть. Только как это проверить?
Ведущий 2. А давай предложим им на время стать сыщиками и детективами.
Ведущий 1. Это как Шерлок Холмс и доктор Ватсон, как инспектор Варнике, что ли? Или как инспекторы Ларин с Дукалисом и Каменская из современных сериалов?
Ведущий 2. Почти. Только они будут математическими детективами.
Ведущий 1. Это как?
Ведущий 2. В математике много таких запутанных заданий, с которыми не справиться без тех качеств, о которых я говорил. Если они смогут выполнить их, то и с настоящими делами, которые распутывают детективы, справятся.
Ведущий 1. Хорошо. Тогда приглашаем на сцену команды детективов из 8 А и 8 Б (команды из 7 человек выходят на сцену и занимают места за своими столиками).
Ведущий 2. Мы выберем из них самых смышленых, а уж им поручим распутать несколько самых сложных дел и выясним, кто из них лучший.
Ведущий 1. Уважаемые команды, претенденты на звание детективов, мы предлагаем вам принять участие в различных конкурсах. На некоторых этапах соревнований проигрывающая на тот момент команда должна будет лишиться одного из игроков. За выполнение каждого задания команда получает определенное количество баллов. Для удобства их подсчета командам выдается определенное число фишек, соответствующее числу набранных баллов. Чтобы зрители могли следить за ходом игры, текущий счет записывается на доске.
Ведущий 2. Не будем зря терять время, предлагаю сразу же перейти к выполнению заданий первого конкурса.
Ведущий 1. Для разминки проверим, насколько наши игроки наблюдательны, что очень важно для детектива.
Ведущий 2. Первое задание на проверку наблюдательности — самое простое. Требуется найти как можно больше отличий на этих двух картинках (демонстрируются две увеличенные картинки из детских развлекательных журналов). Команда получит столько баллов, сколько найдет отличий.
Ведущий 1. Усложняем задание. В нашем зале есть два человека, которые пришли на встречу, но никогда раньше друг друга не видели. Для того чтобы узнать друг друга, у них есть некий предмет, позволяющий их идентифицировать. Попробуйте присмотреться к зрителям в зале и через минуту указать нам на пару этих секретных агентов. (У двоих зрителей в зале одинаковые значки; у одного из них шарфик, а у другого рукавички с одним и тем же узором. Пока команды изучают зал, звучит музыка.)
Ведущий 2. Третье задание. Приглашаем по одному человеку от команды. Сейчас перед вами пройдут ассистенты, в руках у которых папки с изображением разных геометрических фигур (треугольников, квадратов, кругов, отрезков). Вам нужно сосчитать, сколько человек с каким изображением прошло. Появляться они будут в случайном порядке. Например, треугольник, квадрат, треугольник, круг, квадрат, отрезок, квадрат, треугольник. Вы должны вести счет вслух, называя первый треугольник, первый квадрат, второй треугольник, первый круг, второй квадрат и т. д. Сначала дефиле с фигурами проводится для участника из первой команды, потом — для игрока из второй. Ассистенты сами считают, сколько раз они вышли. Если игрок называет ошибочное число, ассистент останавливается. Жюри считает общее количество прошедших людей.
Ведущий 1. Следующее задание. Внимательно посмотрите на рисунок, на котором изображены геометрические фигуры со вписанными в них буквами. Записывать ничего нельзя. Через 10 секунд я убираю этот рисунок и предлагаю другой, на котором в другом порядке изображены фигуры, но уже без букв. Вы должны мысленно вписать в эти фигуры буквы и записать получившиеся слова на листочке. Выигрывает та команда, у которой больше совпадений.

Ведущий 2. Я знаю, что все наши игроки — мастера по рассылке СМС. Так же хорошо они знают и клавиатуру компьютера, поэтому с последним заданием справятся быстро. Какое слово написали, если нажимали на кнопки телефона с цифрами: 282822543, а на клавиатуре компьютера забыли перейти с английского на русский язык и набрали такую комбинацию букв: buhjrf? (Выбывание; игрока.)
Ведущий 1. Слова в последнем задании были зашифрованы не просто так. Пришло время расстаться с одним из членов проигрывающей команды. Прошу участников этой команды подняться и встать в круг. Правила игры таковы. Я повторяю подряд 3 слова: «число» — «фигура» — «имя», указывая каждый раз на нового игрока, потом резко останавливаюсь. Игрок должен быстро, пока я не досчитаю до трех, назвать то слово, на котором я остановился, то есть либо назвать любое число, либо геометрическую фигуру, либо имя математика. Повторяться нельзя. Если игрок не успел этого сделать либо назвал не то, на чем я остановился, или повторил то, что уже говорилось, ему придется покинуть игру.
Ведущий 2. А мы продолжаем игру с оставшимися будущими детективами. Наверняка большинство из вас когда-либо хотели создать систему обмена секретными сообщениями. Криптография — письмо с использованием секретного кода. В ней-то и будут упражняться наши игроки в следующей серии заданий. Ведь коды и шифры широко используются в наше время как в государственной, так и деловой секретной переписке. Существует бесконечное число вариантов шифровки сообщений.
Ведущий 1. Первая шифровка очень простая. Прочитайте, что написано, как можно быстрее: уляралявноляболякойлятраляпеляцииляуглялыляприля осляноляваляниляиляравляныля (убираем лишний слог «ля» и читаем: у равнобокой трапеции углы при основании равны).
Ведущий 2. Разгадывание ребусов — так иногда называют свою работу сыщики и детективы. И мы предлагаем командам разгадать ребусы. Разгадка каждого из них связана с математикой.
Командам выдается по 3 рисунка. Побеждает та, которая прочтет больше слов за 1 мин.
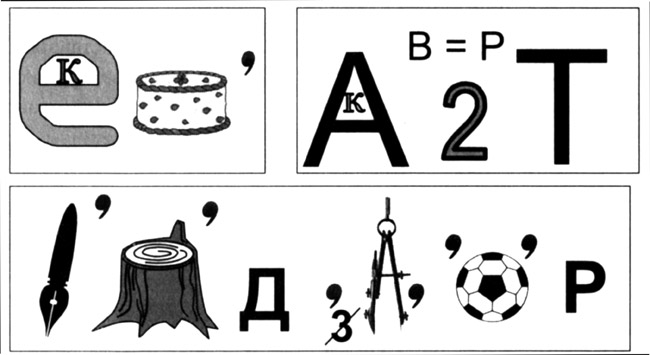
Ответы: вектор, квадрат, перпендикуляр.
Ведущий 1. Для выполнения следующего задания нужно прочитать фразу по первым буквам слов, которые изображены в виде рисунков или условных знаков. Некоторые знаки могут иметь несколько значений, в зависимости от того, в какой отрасли они используются. В этом случае вам нужно выбрать значение для расшифровки.
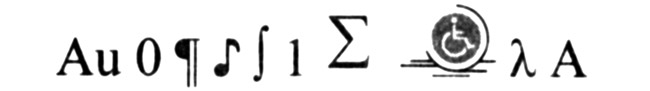
Ответ: золото, ноль, абзац, нота, интеграл, единица, сумма, инвалидная коляска, лямбда, азимут (читается фраза «знание — сила»).
Ведущий 2. Вы когда-нибудь слышали про пиктограммы? Это небольшие схематические рисунки, символически отображающие одно или несколько понятий. В древности до возникновения письменности многие народы пользовались пиктографическим письмом.
Ведущий 1. Игроки получают несколько вариантов стихотворений, связанных с математикой, одно из которых необходимо изобразить с помощью пиктограммы. По одному человеку из команды выходят из зала на 2 мин. За это время оставшиеся члены команды «рисуют» стихотворение. Если, вернувшись, игрок сможет узнать, какое из стихотворений зашифровано, то задание считается выполненным.
Стихотворения для зашифровки:
Можно съесть кило варенья,
Закусить его соленьем,
Не бояться вражьих пуль –
Но нельзя делить на нуль!
И. Кушнир, Л. Финкельштейн
В джунгли прилетела Моль:
«У Осла делитель — ноль».
Звери все подняли вой –
Где делитель взял такой?
Слон сказал не очень строго:
«Пусть идет своей дорогой.
Истину понять изволь:
У ослов — делитель ноль!»
В чащу хмуро Слон ушел,
Пробурчав: «Не прав Осел».
И. Кушнир, Л. Финкельштейн
У человека два плеча,
А в сутках — день да ночка,
Углом назвали два луча
С началом в общей точке.
Н. Зайцева
Медиана
Непрестанно
Выбегает из вершин,
Всех меря на свой аршин.
Лишь прикоснувшись к сторонам,
Она их делит пополам.
О. Панишева
Ведущий 2. А в это время зрители попробуют выиграть приз, продемонстрировав свое внимание. Следите за происходящими в предлагаемой вам задаче событиями и считайте правильно.
Задача. Ты ведешь автобус, в котором находятся 50 пассажиров. Автобус останавливается, 10 человек выходят, 3 входят. На следующей остановке выходят 7, входят 2. Затем на двух остановках выходят по 4 человека, причем на первой садятся 3, а на второй никто не входит. Далее из-за неисправности автобус вновь останавливается. Те, кто спешат, решили идти пешком. Таких оказывается 8 человек. После устранения неисправности автобус приходит на конечную остановку, где все выходят. А теперь ответьте на два вопроса. Первый: сколько остановок сделал автобус? (5.) Второй: как звали водителя автобуса? (Как и отвечающего, ведь в задаче сказано: ты — водитель автобуса.)
Ведущий 1. После этой серии заданий одному из игроков придется покинуть игру. Этим игроком будет тот, чей глазомер оставляет желать лучшего. Чтобы это выяснить, предлагаем каждому из игроков проигрывающей команды записать, какова длина каждого из отрезков, изображенных на рисунке. Выбыть придется игроку, чья суммарная погрешность окажется больше всех.
___________ ___________________ ____ ________________________________
Ведущий 1. Настоящий детектив должен уметь собрать все разрозненные факты воедино и понять, что их объединяет.
• Барабан, охота, математика. (Дробь.)
• Дерево, зуб, слово, арифметические действия. (Корень.)
• Одинцово, Бородино, смородина, Родина. (Число «один», которое есть в записи всех этих слов.)
Ведущий 2. Это задание связано с предыдущим. Нужно найти одно лишнее понятие (формулу, термин, имя) среди предложенных.
1) Арифмометр, абак, калькулятор, амперметр;
2) Виет, Гаусс, Декарт, Ферма;
3) а3 — b3, a2 — b2, а2 + b2, а3 + b3;
4) ромб, трапеция, квадрат, параллелограмм, прямоугольник.
Ведущий 1. В следующем задании необходимо продолжить числовые ряды:
1) 4, 5, 8, 9, 12, 13… (16, 17);
2) 1, 4, 9, 16, 25, 36… (49, 64);
3) 4, 8, 10, 20, 22, 44… (46, 92).
Ведущий 2. А в следующих необычных примерах сможете найти закономерность?
Если господин + подвал = актриса, то сколько будет господин + стрижка + актриса! (Как вариант: семья.)
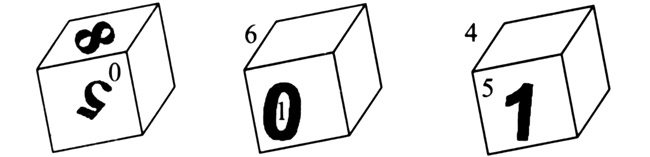
Ведущий 1. И, на мой взгляд, самое сложное задание в этой серии. На гранях кубика нанесены цифры 0, 1,4, 5, 6, 8. Художник нарисовал его в трех положениях. Скажите, какая цифра нанесена на нижней грани (для каждого из трех положений)?
Ведущий 2. Сейчас жюри сообщит количество баллов каждой из команд, так как пришло время попрощаться со вторым игроком. Я попрошу построиться в круг команду, набравшую меньшее число баллов. Каждому из вас я присваиваю номер (выдает номерки на бейджиках, игроки надевают их).
Ведущий 1. A y меня в руках на каждом ходу будет появляться новая функция.
Ведущий 2. Игра носит название «Обманный ход». Я буду задавать самые простые вопросы, адресуя их игроку под номером п и глядя на него. На самом деле ответ на задаваемый вопрос должен дать игрок под номером f(n). То есть если я говорю, что вопрос к игроку под номером 2, а в руках у другого ведущего функция у = х2 — 1, то отвечать должен игрок под номером f(2), то есть под номером 3. Выбывает тот игрок, который ответит невпопад (если его не спрашивали, или если он «прозевает» свой ответ, или если ответит на задаваемый вопрос неправильно). Если после шести вопросов никто не ошибется, то все останутся в игре.
Вопросы:
1) Назовите наибольшее натуральное число.
2) Сколько диагоналей у треугольника?
3) Сколько углов останется у четырехугольника, если один угол у него отрезать?
4) Если на угол величиной в 3° посмотреть в лупу с пятикратным увеличением, какой величины будет угол?
5) Можно ли из прутьев длиной 2, 3 и 4 см выложить прямоугольный треугольник?
6) Какой знак поставить между 4 и 5, чтобы получилось число, большее 4, но меньшее 5?
Ведущий 1. Не последнюю роль в расследовании запутанных дел играет интуиция. Проверим, как она сможет помочь нашим игрокам. Прошу обе команды выстроиться в колонну по одному в произвольном порядке. Я сообщаю вам некоторую информацию, затем называю число. Как это число связано с вышеназванной информацией, вам должна подсказать интуиция. Будут даны два варианта ответа. Если вы выбираете первый, шагаете влево, второй — вправо. Те, кто выбрали неправильный ответ, присаживаются на свои места. Количество баллов будет соответствовать количеству оставшихся в строю после последнего вопроса игроков (правильные ответы выделены курсивом).
1. Геометрию, которую мы учим в школе, называют евклидовой геометрией. Число 13.
а) 13 книг включают «Начала Евклида».
б) 13 раз переиздавалась эта книга.
2. Сегодня мы не мыслим свою жизнь без телефонной связи. А изобрел телефон американец инженер и учитель Александр Грэхем Белл. Число 28.
а) 28 лет было изобретателю.
б) 28 абонентов соединяла первая телефонная станция.
3. Рельсы, а с точки зрения математики — две параллельные прямые, по которым бегут поезда, впервые появились в Англии. Число 1,44.
а) Такова длина (в км) первого отрезка пути, построенного для паровоза с колесами.
б) Такова ширина (в м) колеи почти во всех странах мира.
4. Этот блестящий круг (показывает компакт-диск) сегодня знаком даже первокласснику. А ведь было время, когда ЭВМ были размером с комнату, а многие взрослые и представить не могли, что тома энциклопедий смогут уместиться на вот это тоненькое чудо. Число 74.
а) 74 минуты длилась запись на первом компакт-диске, ведь именно столько звучала 9-я симфония Бетховена, которого очень любил президент компании, создавшей первый компакт-диск.
б) 74 см составлял диаметр первого компакт-диска.
5. Пифагор считал, что все на свете можно выразить числом. Известно, что у него была своя школа, которая одновременно являлась и религиозным союзом, и политическим клубом, и научным сообществом. Эмблемой пифагорейцев была пентаграмма — пятиугольная звезда, вписанная в окружность, которую они назвали символом здоровья. Число 17.
а) Было любимым у пифагорейцев, так как правильный 17-угольник можно вписать в окружность с помощью циркуля и линейки и с 17 лет принимали учеников в школу Пифагора.
б) Его пифагорейцы не любили, считали презренным числом и избегали его.
6. Известно, что многие математики потратили не один год своей жизни, чтобы вычислить значение числа п — отношения длины окружности к ее диаметру. Один из этих ученых — Лудольф ван Цейлен. Число 32.
а) 32 года потратил ученый на вычисление значения этого числа.
б) Это число с 32 знаками после запятой выгравировано на его надгробии.
7. Карл Фридрих Гаусс — тот, кого при жизни называли королем математики, называл математику царицей всех наук. Число 19.
а) В этом возрасте он сделал выбор между филологией и математикой в пользу последней.
б) Знал 19 языков.
Ведущий 2. Поздравляю тех, у кого развита интуиция. Прошу все команды занять свои места.
Ведущий 1. А я интуитивно чувствую, что задания с каждым туром усложняются, при этом игроков становится все меньше и меньше.
Ведущий 2. Ты прав. Прошу подойти игроков проигравшей команды. Отбор выбывающего игрока будет проведен с помощью игры на скорость.
Ведущий 1. Перед вами 5 блокнотов (или ящичков), закрытых на ключ. Ключи ко всем разные. А вот примерно 20 ключей, на каждом из которых стоит номер. Вам нужно за 1 минуту подобрать нужный ключ, открыть блокнот и на первой странице прочитать загадку, в которой пропущено число, написанное на ключе. Отгадав загадку, нужно выбрать одну из 50 картинок, на которой изображена отгадка к вашей загадке. Кто не успеет — выходит из игры. Возможно, это будет не один человек. Успеют все — все останутся. Прежде чем начать отсчет времени, предлагаю внимательно изучить свой замочек, чтобы быстрее выбрать ключ.
Ведущий 2. А мы продолжаем проверять имеющиеся у игроков качества, крайне необходимые настоящим детективам. Следующее из них — память. Я в течение 10 секунд показываю рисунок, который потом в течение 30 секунд команды должны будут воспроизвести на листах бумаги. Это задание на проверку вашей коллективной памяти, так как нужно предоставить один рисунок от всей команды. А рисунок этот будет таким:
Ведущий 1. Второе задание связано со старинным методом, который использовался до возникновения письменности или когда нужно было передать знания, которые запрещалось записывать. Это был очень эффективный метод: многие знания в течение целых тысячелетий не были утрачены.
Ключ и секрет этого метода — в частом повторении. Например, индийские учителя повторяли ученику одну строчку до тех пор, пока слова и их значения не отпечатаются в уме. Ученик должен был повторить строчку как в прямом, так и в обратном порядке и знать место каждого слова. На следующий день прибавляли новую строку. И так каждый день, не забывая повторять предыдущие. Это система, по которой в древности запоминали книги, равные по объему Библии!
Ведущий 2. Вам предлагается формулировка теоремы длиной всего в одну строку: «У любого параллелограмма сумма квадратов диагоналей равна сумме квадратов всех его сторон». Каждый игрок должен повторить теорему вслух. А теперь по очереди выполните следующие задания:
1) Какое слово стоит в формулировке на пятом месте? (Предлоги тоже считаются.)
2) Назовите последнее слово теоремы.
3) Сколько слов в теореме?
4) Прочитайте теорему наоборот, начиная со слова, стоящего в конце формулировки.
Ведущий 1. Для следующего задания нужно уметь не только запоминать, но и хорошо считать. Задача такова: запомнить 5 чисел, затем в уме сложить первое число со вторым, полученную сумму записать, второе число сложить с третьим — сумму записать, третье число сложить с четвертым — сумму записать, четвертое число сложить с пятым — сумму записать. То есть на листочке должно быть записано всего 4 суммы. Игроки выходят по очереди. Играют столько раз, сколько игроков в меньшей по численности команде. Время для вычисления — 15 секунд.
Числа:
1) 5, 2, — 7, 1, 4; 4) 2, 6, — 2, 5, 3;
2) 3, — 5, 6, 2, 5; 5) 4, 4, 6, 1, — 7.
3) 7, 1, 4, — 3, 2;
Ведущий 2. «Что изменилось?» — так называется следующее задание на проверку памяти.
Ассистенты выносят стол, на котором выставлены несколько стереометрических фигур, накрытых тканью: шар, конус, цилиндр, куб, параллелепипед, усеченный конус, призма. Игроки подходят к столу. На 2-3 с ткань приподнимается. Затем ведущий либо убирает некоторые предметы, либо меняет их местами, так чтобы не видели участники. Ткань поднимается снова. Игроки должны заметить произошедшие перемены.
Ведущий 1. Подведем промежуточные итоги.
Игроки становятся в круг. Ведущий не спеша делает разные гимнастические движения. Играющие повторяют те же движения, но с отставанием на два. При первом и втором движениях ведущего они стоят неподвижно, при третьем — повторяют первое, при четвертом — второе и т. д. Тот, кто перепутает движения, выбывает из игры.
Ведущий 2. Среди других «крепостей царства смекалки» логические задачи стоят особняком. С одной стороны, они отличаются от большинства задач-загадок тем, что в них нет игры слов, попыток ввести читателя в заблуждение. С другой стороны, отличаются от математических задач тем, что для их решения требуется сообразительность, а не запас каких-то специальных знаний.
Ведущий 1. Предлагаю обеим командам решить следующую задачу. (Читает условие задачи, а затем раздает текст.) Победит та команда, которая справится с задачей быстрее.
Задача. Воронов, Павлов, Левицкий и Сахаров — 4 талантливых молодых человека. Один из них — танцор, другой — художник, третий — певец, а четвертый — писатель. О них известно следующее: Воронов и Левицкий сидели в зале консерватории в тот вечер, когда певец дебютировал в сольном концерте. Павлов и писатель вместе позировали художнику. Писатель сочинял биографическую повесть о Сахарове и собирается написать о Воронове. Воронов никогда не слышал о Левицком. Кто чем занимается? (Сахаров — художник, Левицкий — писатель, Воронов — танцор, Павлов — певец.)
Ведущий 2. Попрошу ассистента вынести условие следующей задачи. (На подносе — 6 стаканов. 3 из них пустые, а в 3 налита вода. Сначала стоят 3 заполненных водой стакана.) Сделайте так, чтобы пустые и полные стаканы чередовались. Брать в руки разрешается только один стакан. Через минуту вы должны продемонстрировать, как это можно сделать. (Решение: взять второй полный стакан и перелить из него воду во второй пустой.)
Ведущий 1. Умение логически рассуждать может пригодиться людям любой профессии. Предположим, что таможеннику поступила информация, что коллекционер провозит среди 8 настоящих монет одну фальшивую. Таможенник, чтобы не вызвать подозрений и не задерживать очередь, может произвести не более двух взвешиваний. Как он может определить, какая из монет фальшивая, если к тому же отключили электричество и электронные весы не работают, взвешивать можно только на чашечных? (Решение: положить на чашки по 3 монеты. Если чаши весов уравновесились, то фальшивая находится среди оставшихся двух, что легко определяется следующим взвешиванием. Если одна из чаш перевесила, взвешиваем 2 из этих трех монет по одной на каждой чаше весов, остается третья.)
Ведущий 2. Когда мы рассуждаем, то, чтобы сделать некоторый вывод, пользуемся стандартными схемами, иногда даже не замечая этого. Например, рассмотрим такое рассуждение. Любое натуральное число — целое. 3 — натуральное, значит, 3 — целое.
Схема этого рассуждения такова:
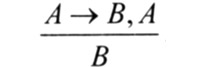
где над чертой записаны посылки этого рассуждения, а под чертой — вывод. Заметим, что это рассуждение является дедуктивным, то есть при использовании такой схемы из истинных посылок обязательно получится истинный вывод. А вот следующее рассуждение, очень похожее на предыдущее. Любое натуральное число — целое. 5 — целое, значит, 5 — натуральное. На первый взгляд, и тут все правильно. Но схема немного другая:
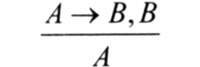
Попробуем теперь по этой же схеме порассуждать с другими числами. Любое натуральное число — целое. -2 — целое, значит, -2 — натуральное. И что мы видим? Вывод неправильный! Значит, рассуждение по такой схеме недедуктивное.
Ведущий 1. В следующем задании игрокам будет предложено несколько рассуждений. Вам необходимо вычеркнуть все рассуждения, которые вы считаете недедуктивными, а из первых букв последних слов в оставшихся дедуктивных рассуждениях образуется слово. Вы должны его отгадать.
(Рассуждения выдаются на листочках каждой команде.)
Рассуждения (недедуктивные выделены курсивом):
1. У всех птиц два крыла. У самолета два крыла. Значит, самолет — птица.
2. Если многоугольник правильный, то в него можно вписать окружность. Квадрат — правильный многоугольник, значит, в квадрат можно вписать окружность.
3. Если у многоугольника нет диагоналей, то он является треугольником. В данном многоугольнике нет диагоналей. Значит, данный многоугольник — треугольник.
4. Любое млекопитающие имеет желудок. Окунь не млекопитающее. Значит, у окуня нет желудка.
5. В нашей школе принято, что на все праздники девочки надевают белые блузки. Сегодня праздник — День учителя. Значит, сегодня все девочки будут в белых блузках.
6. В нашей школе принято, что на все праздники девочки надевают белые блузки. Сегодня все девочки в белых блузках. Значит, сегодня праздник.
7. В нашем классе каждый, кто занимается в кружке юных математиков, — отличник. Вася занимается в кружке юных математиков. Значит, Вася — отличник.
8. Любое дерево — растение. Дуб — дерево, значит, дуб — растение.
9. Любое дерево — растение. Дуб — растение, значит, дуб — дерево.
10. Любое дерево -растение. Мак — растение, значит, мак — дерево.
Ведущий 2. Итак, если команды успешно справились с заданием, то они должны были прочитать слово «отбор», что означает, что пришло время в последний раз выбрать игрока, которому предстоит покинуть игру.
Ведущий 1. А сделаем мы это снова с помощью игры. Игроки располагаются вокруг стола, на котором на некотором расстоянии друг от друга разложены 6-7 бумажных листочков с изображением на них формул сокращенного умножения. Я называю формулы, например, разность квадратов, и быстро кладу руку на листочек с изображением этой формулы. Одновременно со мной должны положить руку на этот листочек и все играющие. Неожиданно для вас я на одном из ходов кладу руку не на ту формулу, которую назвал. Те, кто ошибутся, выбывают из игры.
Ведущий 2. Как детективам удается распутывать сложные преступления? Путем регулярной тренировки своего мышления. В том числе они учатся и на уже раскрытых делах. То есть кто-то до них собрал все факты воедино, опросил свидетелей и сделал вывод. Будущим детективам предоставляется все, кроме вывода. Как получен этот вывод, им предстоит догадаться самим. Догадаться, используя простейший житейский опыт, предстоит и при изучении следующего дела. Если команды не смогут его раскрыть, возможно, это сделает кто-то из зрителей. Если зрителю это удастся, он сможет отдать заработанный балл любой команде.
Дело об ограблении на даче
С наступлением затяжных холодов семейство Ивановых покинуло дачу и вернулось в свою городскую квартиру. Еще до переезда хозяин дачи договорился со своим соседом Петровым, чтобы тот присматривал за его хозяйством. Через несколько дней после Нового года Петров позвонил Иванову и сообщил, что дача ограблена. Иванов нанял частного детектива, и вскоре сыщик уже допрашивал Петрова. Тот рассказал следующее: «Ночью я услышал подозрительный шум. Несмотря на сильный мороз, я сразу поднялся и отправился к даче соседа. Я заглянул в окно, но все стекла замерзли, и я ничего не смог увидеть. Тогда я продышал небольшую дырочку во льду, покрывавшем оконное стекло, и посветил карманным фонариком. В комнате был страшный беспорядок. На следующее утро я позвонил Иванову и все рассказал».
«Все ясно, — заметил детектив. — Попрошу вас следовать за мной».
Почему детектив заподозрил Петрова в краже?
Ответ: оконные стекла замерзают изнутри, а не снаружи. Продышать с улицы «глазок» в окне невозможно. На этом Петров и попался.
Ведущий 1. После такой тренировки на житейском материале переходим к распутыванию математических дел. Настоящий детектив справился бы с предложенным заданием в два счета и рассудил спорящих по справедливости. А вы?
Выходят две пары заранее подготовленных учеников. Спорят: «Я прав». — «Нет, я».
Ведущий. Не спорьте, обратитесь к нашим детективам, и они вас рассудят.
1-й ученик. Вот скажите: правильно записать, что 5 + 7 будет «адиннадцать».
2-й ученик. Вы сами видите, какой он безграмотный! Правильно писать «одиннадцать», вы согласны со мной?
Ведущий. Ну и кто прав, уважаемые детективы? (Никто, ведь 5+7= 12.)
3- й и 4-й ученики. У нас тоже возник спор по правописанию. Как правильно сказать: 2/3 + 3/4 равно 1 7/12 или 2/3 + ¾ равняется 1 7/12 ? (2/3 +3/4 ≠ 1 7/12)
Ведущий. Справившись с такими простыми заданиями, переходим к рассмотрению серьезных дел. Их всего 5. От того, сколько из них вы сможете раскрыть за 5 минут, зависит победа или проигрыш команды. Ведь это финальное и потому самое сложное задание. Вот вам и заявители. Прошу вас, ознакомьте наших сыщиков подробнее с вашим делом. А вы внимательно выслушайте заявителей и составьте протокол: запишите то, что считаете нужным, как можно подробнее, чтобы не упустить ни одной важной детали.
Дело №1.
Заявитель. Я пришел запатентовать свое открытие: как с помощью математики, а именно пропорции, вычислять вопросы падежей.
Например, родительный падеж: вопросы — кого? чего? Дательный: первый вопрос — кому? А чтобы вычислить второй, составляю пропорцию: кого относится к кому как чего относится к x. Находим x :
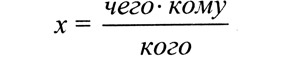
Сокращаем на ко и го и получаем чему – второй вопрос дательного падежа. Чем не открытие? А они отказали. Разрешите мою проблему.
Дело №2.
Заявитель. Когда нас учили сокращать дроби, то всегда обращали внимание, что слагаемые сокращать нельзя, а можно только множители. А я пришел к выводу, что можно. Вот, смотрите. Я беру дробь
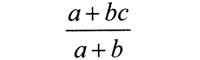
и пишу:
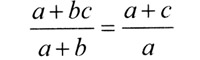
Вы скажете, что это глупости? Вовсе нет. Вот, например, если взять а = 6, b = 2, с = 3 и подставить в эти дроби. Смотрите, что получается.
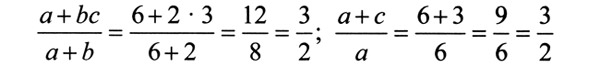
По-вашему это случайно? А возьмите теперь а = 2, b = 3, с = 6. Тоже все получается. Ну как, можно сокращать слагаемые или все-таки нельзя?
Дело №3.
А. Дело началось с того, что мы приступили к выполнению домашнего задания, в котором выносили множители из-под знака корня. Посмотрите, я ведь все сделал правильно?
Пишут на доске или показывают заранее заготовленный плакат.
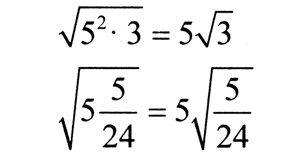
Б. А я ему говорю, что второй пример так решать нельзя — нужно писать подробно, как нас учили:
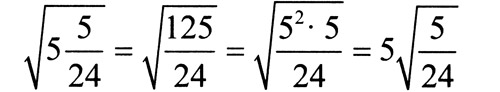
А. Но ответ у тебя получился такой же, как и у меня. Тогда зачем мучиться: вынес целую часть — и все, так же быстрее.
Б. А если другие числа будут, ты считаешь, что ответ тоже совпадет?
А. Я уверен в этом. Ведь в следующем примере у меня тоже все вышло.
Проверь сам:
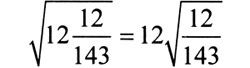
Б. Что-то здесь не так, а что — никак не пойму.
Ведущий. Помогите ученикам, раскройте, в чем тут дело и всегда ли можно так выносить множитель из-под знака корня?
Разгадка: ответ получится правильным при таком вынесении, только если подкоренное выражение подобрано по формуле
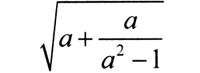
Дело №4.
Заявитель. Мы в школе доказывали теорему, что из точки на прямой можно восстановить только один перпендикуляр. Учили также, что угол, опирающийся на диаметр, прямой. А я вот взял циркуль и смог провести два перпендикуляра к прямой. Неужели какая-то из теорем была сформулирована в школьном учебнике неправильно? Смотрите, что получается (демонстрирует рисунок).
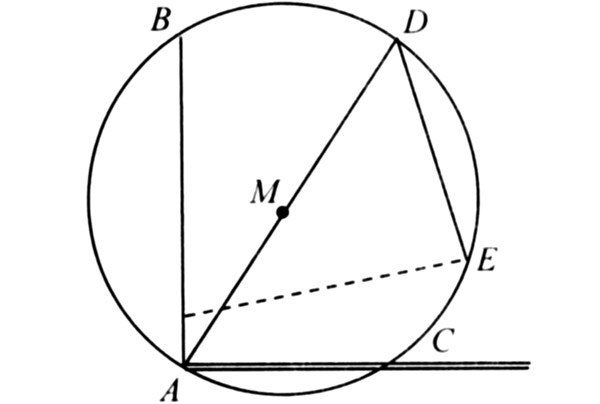
Через вершину прямого угла ВАС проведем произвольный отрезок AD. Отметим середину этого отрезка — точку М. И на AD, как на диаметре, построим окружность с центром в точке М. Из точки D проведем DE || АВ до пересечения с окружностью в точке Е. Соединим точки А и Е и получим прямой угол AED. Так как DE || АВ, то угол BAС также прямой. Но угол BAC тоже прямой по условию. Значит, и линия АС, и линия АЕ будут перпендикулярны линии АВ, то есть из точки А к линии АВ могут быть восстановлены два перпендикуляра. В чем тут дело?
Ответ: проведя из точки D параллель отрезку АВ, заметим, что при его пересечении с прямой АС получится прямой угол, опирающийся на AD. AD, в свою очередь, будет гипотенузой для получившегося треугольника. Окружность, построенная на AD, как на диаметре, пройдет через точку, находящуюся на АС, а потому никогда не пересечет DE в точке Е. Значит, чертеж выполнен неправильно.
Дело №5.
Заявитель. А вам не приходило в голову, что все числа равны между собой? Это можно доказать. Вот я беру два произвольных числа, причем а > b. Обозначим разность этих чисел буквой с, то есть a – b = c,a = b + c. Умножим обе части последнего равенства на (a- b): а2 — ab = ab + ас- b2 — bс.
Вычтем из обеих частей ас: а2 — аb — ас = ab — b2 — bс.
Вынесем общие множители за скобку: а(а – b — с) = b(а – b — с).
Делим обе части на (а — b — с). Получаем, что а = b. То есть два произвольно взятых числа а и b, меньшее а, равны друг другу. (Ошибка в делении на выражение а – b — с = 0; софизмы.)
Ведущий. А пока наши игроки размышляют над такими непростыми делами, зрителям предлагается назвать самого лучшего игрока сегодняшней игры, который получит приз зрительских симпатий. Для этого им нужно написать имя игрока на листочке и опустить записку в коробочку, которую проносит вдоль зрительских рядов ассистент.
Подведение итогов игры. Награждение победителей.
Чтец.
Нас математика учит
Думать, творить, рассуждать.
Без этой важной науки
Детективом, поверьте, не стать.
И дело не в формулах даже,
А как тренируется мозг.
Математика всем нам подскажет
Ответ на сложный вопрос.
Чтоб до истины докопаться,
Путь нелегкий нужно пройти.
А математика, братцы,
Помощник на этом пути.




 Внеклассное мероприятие по математике 8 класс к неделе математики
Внеклассное мероприятие по математике 8 класс к неделе математики