2 новых тренировочных варианта ЕГЭ 2026 по математике профильный уровень задания и ответы с решением по новой демоверсии ФИПИ для подготовки к экзамену. Каждый вариант состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 12 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
1. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
3. От треугольной пирамиды, объём которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объём отсечённой треугольной пирамиды.
4. Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
5. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось ровно два броска? Ответ округлите до сотых.
6. Найдите корень уравнения (2𝑥 − 5)2 = (2𝑥 + 2)2 .
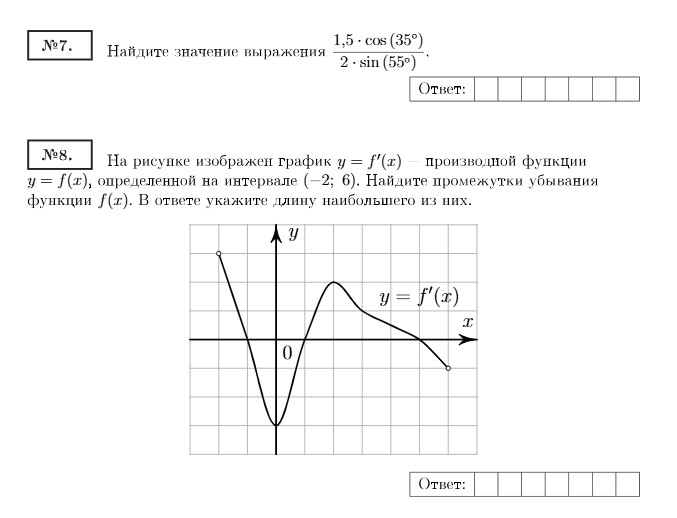
8. На рисунке изображен график 𝑦 = 𝑓 ′ (𝑥) — производной функции 𝑦 = 𝑓(𝑥), определенной на интервале (−2; 6). Найдите промежутки убывания функции 𝑓(𝑥). В ответе укажите длину наибольшего из них.
9. Высота над землей подброшенного вверх мяча меняется по закону ℎ(𝑡) = 1,8 + 8𝑡 − 5𝑡 2 , где ℎ — высота в метрах, 𝑡 — время в секундах, прошедшее с момента броска. Через сколько секунд после броска мяч окажется на той же высоте, с которой начал движение?
10. Почтальон выехал из пункта 𝐴 в 16.00 и должен доехать до пункта 𝐵 к 19.00. Однако, проехав треть пути, почтальон обнаружил, что забыл посылку. Во сколько раз нужно увеличить скорость почтальону, чтобы, вернувшись за посылкой, прибыть в 𝐵 к назначенному времени?
11. На чертеже изображены графики двух квадратичных функций с целыми коэффициентами. Графики пересекаются в точках 𝐴 и 𝐵. Найдите ординату точки 𝐵.
14. В правильной четырехугольной пирамиде 𝑆𝐴𝐵𝐶𝐷 сторона основания равна 12, высота 𝑆𝐻 равна 6 √ 3. Точка 𝐾 — середина бокового ребра 𝑆𝐷, а точка 𝑁 — середина ребра 𝐶𝐷. Плоскость 𝐴𝐾𝐵 пересекает боковое ребро 𝑆𝐶 в точке 𝑃. а) Докажите, что прямая 𝐾𝑃 пересекает отрезок 𝑆𝑁 в его середине. б) Найдите расстояние от точки 𝑃 до плоскости 𝑆𝐴𝐵.
16. В июле 2026 года планируется взять кредит на пять лет в размере 3,3 млн руб. Условия его возврата таковы: каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле 2027, 2028 и 2029 годах долг остаётся равен 3,3 млн руб.; платежи в 2030 и 2031 годах должны быть равны; к июлю 2031 года долг должен быть выплачен полностью. Найдите разницу между последним и первым платежами.
17. На стороне 𝐵𝐶 параллелограмма 𝐴𝐵𝐶𝐷 выбрана точка 𝑀 такая, что 𝐴𝑀 = 𝑀𝐶. Точка 𝑂 — центр окружности, вписанной в треугольник 𝐴𝑀𝐷. а) Докажите, что точка 𝑂 лежит на диагонали 𝐴𝐶. б) Найдите 𝑀𝐷, если 𝐴𝐵 = 3, 𝐵𝐶 = 5 , ∠𝐵𝐴𝐷 = 60∘ .
19. Дано натуральное число. К этому числу можно либо прибавить утроенную сумму его цифр, либо вычесть утроенную сумму его цифр. После прибавления или вычитания суммы цифр, число должно остаться натуральным. а) Можно ли получить из числа 128 число 29? б) Можно ли получить из числа 128 число 31? в) Какое наименьшее число можно было получить из числа 128?
296 тренировочный вариант ЕГЭ 2026
1. Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
4. В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 8 спортсменов из Сербии, 3 спортсмена из Хорватии и 6 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Сербии.
5. По отзывам покупателей Василий Васильевич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,84. Вероятность того, что этот товар доставят из магазина Б, равна 0,7. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
10. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
16. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы: • каждый январь долг возрастает на r% по сравнению с концом предыдущего года; • с февраля по июнь каждого года необходимо выплатить часть долга. Известно, что кредит был полностью погашен за два года, причём в первый год было переведено 75 000 рублей, а во второй год—46 000 рублей. Найдите число r.
19. Даны n различных натуральных чисел, составляющих арифметическую прогрессию. а) Может ли сумма всех данных чисел быть равной 16? б) Каково наибольшее значение n, если сумма всех данных чисел меньше 900? в) Найдите все возможные значение n, если сумма всех данных чисел равна 235.




 Вариант 1А
Вариант 1А