Школьный этап Сириус по Математике для 4-ой группы 17 октября 2025 г.
Вопросы и ответы 4 класс
Задание 1. Дети играют в «горячую картошку». Настя передавала мяч дважды Косте и Лене. Оля передала мяч Насте. Маша тоже передала мяч Насте, а получила его от Кости. Больше никто никому мяч не передавал.
У кого мяч сейчас?
У Кости
У Лены
У Маши
У Насти
У Оли
У кого мяч был изначально?
У Кости
У Лены
У Маши
У Насти
У Оли
Задание 2. Три слона весят столько же, сколько двенадцать бегемотов, а один кит весит столько же, сколько пять слонов. Сколько бегемотов уравновесят одного кита?
Задание 3. У Пети есть белый квадрат 6×6.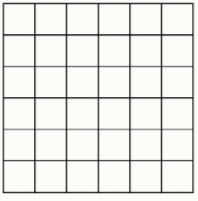
Его младший брат Вася закрасил 15 клеток в чёрный цвет и, чтобы скрыть свои проделки, согнул квадрат пополам вдоль вертикальной линии. Клетки, которые совмещаются при сгибании с окрашенными, тоже становятся чёрными. Вечером Петя развернул свой квадрат.
Какое наибольшее число чёрных клеток он мог увидеть?
Какое наименьшее число чёрных клеток он мог увидеть?
Задание 4. У Маши есть пять развёрток кубика. Из каких развёрток можно склеить куб, в котором три чёрные грани примыкают к одной вершине? Выберите все подходящие варианты: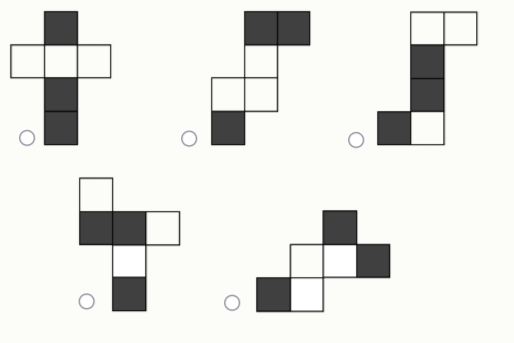
Задание 5. Есть равное количество шоколадных плиток двух видов. Первый вид с размерами 2×4 дольки , второй вид 3×6 долек. Всего 234 дольки. Петя хочет разломить плитки на куски по две дольки. За один раз можно взять любой кусок и разломить его по границам долек на две части. Сколько разломов ему придётся сделать?
Задание 6. Повар разрезает прямоугольный пирог прямыми разрезами. Каждый раз он берёт один из имеющихся кусков и делит его на две части. В какой‑то момент повар останавливается и подсчитывает все углы всех полученных кусков. Их оказывается 25. Какое минимальное количество разрезов могло быть сделано?
Задание 7. Первого сентября учитель проводил в классе опрос. В классе 30 учеников. Всех детей можно разделить на три типа: некоторые всегда лгут, некоторые всегда говорят правду, а некоторые попеременно лгут и говорят правду. Последние произвольно выбирают свой первый ответ либо ложь, либо правду, но каждое последующее утверждение имеет значение, противоположное по истинности предыдущему. Учитель каждому задал одни и те же три вопроса:
1. «Ты всегда говоришь правду?»
2. «Ты чередуешь правду и ложь?»
3. «Ты всегда лжёшь?»
Каждый ответ «да» учитель отмечал в опросном листе плюсиком. За ответы на первый вопрос он поставил 25 плюсиков, на второй 19, на третий 16.
Сколько детей всегда лгут?
Сколько детей всегда говорят правду?
Сколько детей чередуют правду и ложь?
Задание 8. Маша пришла в картинную галерею. На схеме каждый зал обозначен квадратом. Любые два соседних зала соединены дверью. Маша хочет пройти от входа до выхода, обозначенных буквами A и B B соответственно. Каждый раз она переходит по схеме либо в зал правее, либо в зал ниже. Сколько залов посетит Маша? Не забудьте учесть залы A и B .
Сколько у неё способов это сделать?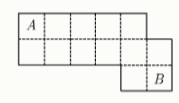




 Задания
Задания