Олимпиадные задания по математике 5 класс с решениями и ответамиОлимпиада по математике (5-6 классы) с ответами
I тур
Задача 1.
В летний лагерь приехали 3 друга: Миша, Володя и Коля. Известно, что каждый из них имеет одну из фамилий: Иванов, Семёнов и Петров. Миша не Петров; отец Володи — инженер, Володя учится в 6-м классе. Мальчик с фамилией Петров учится в 5-м классе. Отец с фамилией Иванов — слесарь. Какая фамилия у каждого из ребят?
Задача 2.
4 карандаша и 3 общих тетради стоят 54 рубля, а 2 карандаша и 2 общих тетради стоят 34 рубля. Сколько стоят 8 карандашей и 7 общих тетрадей?
Задача 3.
На каждой перемене Пончик съедает 2 пончика, а Фантик выпивает стакан «Фанты». Сколько пончиков и стаканов «Фанты» они съедают и выпивают на переменах с понедельника по субботу включительно, если за это время у них было по расписанию 35 уроков?
Задача 4.
Разрезать фигуру, составленную из 5 квадратов, на части, из которых можно сложить ровно один квадрат.
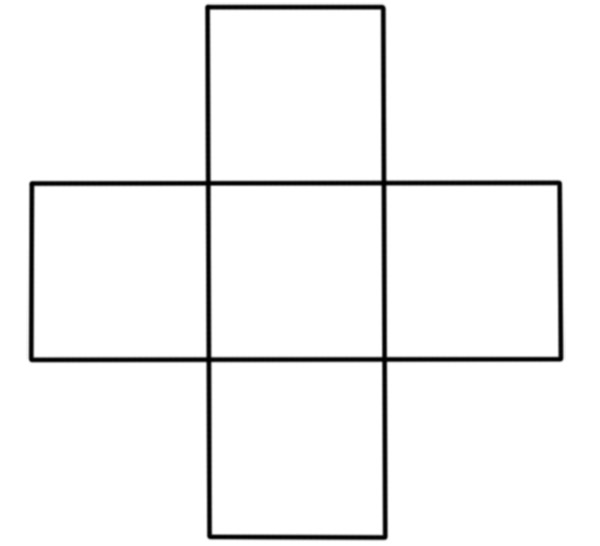
Задача 5.
Сможет ли Катя посадить 8 цветков в 7 рядов по 3 цветка в каждом ряду?
Задача 6.
Вини-Пух, Сова, Кролик и Пятачок вместе съели 70 бананов, причём каждый из них съел хотя бы один банан. Вини-Пух съел больше всех; Сова и Кролик вместе съели 45 бананов. Сколько бананов съел Пятачок?
Ответы
Задача 1.
Миша Иванов, Володя Семёнов, Коля Петров.
Задача 2.
4 к. + 3 т. = 54 (руб.); 2 · (2 к. + 2 т.) = 2 · 34 (руб.). Сложив два равенства, получим: 8 к. + 7 т. = 54 + 68 = 122 (рубля).
Задача 3.
Если бы все 35 уроков шли подряд, перемен было бы 34. Но из них надо исключить промежутки между последним уроком одного дня и первым уроком другого дня. Таких промежутков 5, и перемен у Пончика и Фантика — 29. Поэтому Пончик съедает 58 пончиков, а Фантик выпивает 29 стаканов «Фанты».
Задача 4.
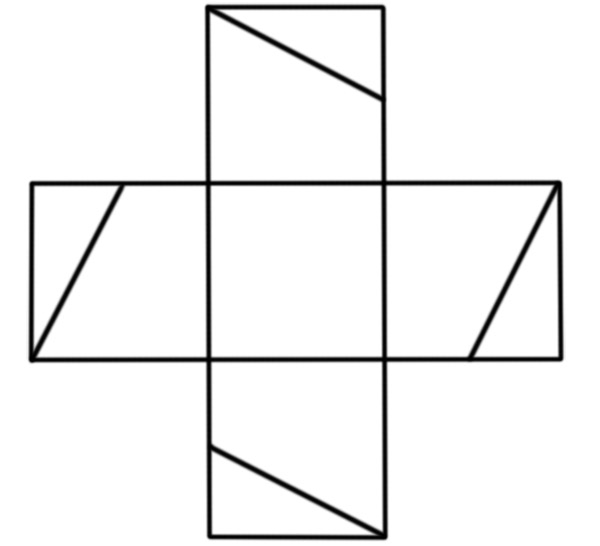
Задача 5.
Да, сможет. Например, так:
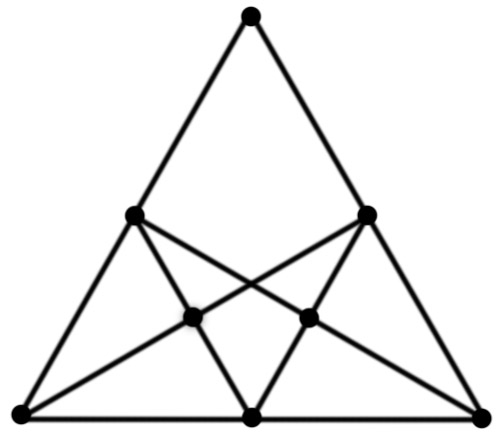
Задача 6.
Вини-Пух и Пятачок вместе съели 25 бананов. Так как Пятачок съел по крайней мере 1 банан, то Вини-Пух съел не более 24 бананов. Тогда в паре Сова — Кролик кто-то съел 23 банана, а кто-то — 22 банана (меньше не может быть, так как тогда второй в паре съест по крайней мере 24 банана, то есть не меньше, чем Вини-Пух).
Следовательно, Вини-Пух съел 24 банана, а Пятачку достался всего один банан.
II тур
Задача 1.
В магазине было 8 пил, а топоров — в 3 раза больше. Одной бригаде продали половину топоров и 3 пилы за 84 р. Оставшиеся топоры и пилы продали за 100 рублей другой бригаде. Сколько стоит 1 топор и 1 пила?
Задача 2.
4 ученика, Андрей, Борис, Владимир и Геннадий, заняли первые 4 места на районной математической олимпиаде, причём никакие двое не делили между собой какие-либо 2 места. На вопрос, какое место занял каждый из них, участники дали по 2 разных ответа, причём в каждом из ответов одна часть истинная, другая — ложная. Какое место занял каждый?
а) Боря — II, Андрей -I;
б) Андрей — II, Геннадий — III;
в) Владимир — II, Геннадий — I.
Задача 3.
Геологи нашли 7 камней, массы которых равны 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг, 7 кг. Эти камни разложили в 4 рюкзака так, что в каждом рюкзаке масса была одинаковой. Как они это сделали?
Задача 4.
В одном озере растёт волшебная лилия. Её размеры увеличиваются каждый день ровно в 2 раза. Если посадить одну такую лилию в пруд, то через 20 дней она заполнит его полностью. За сколько дней весь пруд закроется, если сразу посадить четыре таких лилии?
Задача 5.
Два всадника едут навстречу друг другу: один со скоростью 12 км/ч, а другой — на 3 км больше. На каком расстоянии они будут через 2 часа после встречи?
Задача 6.
Имеется 20 конфет в различных обёртках: 3 штуки — в красных, 3 штуки — в фиолетовых, 5 штук — в синих, 9 штук — в коричневых. Какое наименьшее количество конфет надо взять наудачу, чтобы среди них обязательно были 4 разных конфеты?
Ответы
Задача 1.
(12 т. + 5 п. = 100) — (12 т. + 3 п. = 84); 2 топора стоят 16 р.; 1 пила = 8 р.; 1 топор = 5 р.
Задача 2.
Андрей — I место; Владимир — II место; Геннадий — III место; Борис — IV место.
Задача 3.
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (кг) — масса всех камней; 28 : 4 = 7 (кг) — в каждом рюкзаке; камни положили так: 7 кг; 6 + 1 (кг); 5 + 2 (кг); 4 + 3 (кг).
Задача 4.
Если посадить в пруд одну лилию, то через 2 дня будут 4 лилии, а ещё через 18 дней лилии заполнят его полностью. Следовательно, если сразу посадить 4 таких лилии, то весь пруд закроется за 18 дней.
Задача 5.
После встречи всадники поедут в разные стороны из одного и того же пункта; за 2 часа один проедет 24 км, а другой — 30 км; следовательно, расстояние между ними будет 24 + 30 = 54 (км).
Задача 6.
9 + 5 + 3 + 1 = 18 (конфет).
III тур
Задача 1.
В зоопарке живут 30 обезьян. 10 из них берут от посетителей конфеты, 15 — печенье, а 9 предпочитают не брать ничего. Сколько обезьян берут у посетителей и конфеты, и печенье?
Задача 2.
В записи 1 2 3 4 5 6 7 8 9 поставить знаки « + » и « — » так, чтобы значение выражения равнялось 100.
Задача 3.
Расставьте в свободных клетках числа 4, 5, 6, 7, 8, 9 так, чтобы сумма чисел в каждом столбце и в каждой строке равнялась 15.
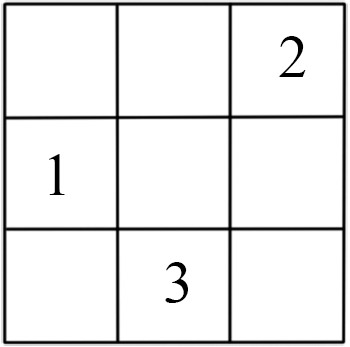
Задача 4.
Какие цифры надо вставить вместо звёздочек?
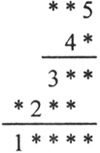
Задача 5.
Мышь, мышонок и сыр в мышеловке весят вместе 180 г. Мышь весит на 100 г больше, чем сыр и мышонок вместе. Сыр весит в 3 раза меньше, чем мышонок. Сколько весит каждый из них?
Задача 6.
Написать 55, употребляя 5 четвёрок.
Ответы
Задача 1.
30 — 9 = 21 (обез.) — берут что-то одно; 10 + 15 — 21 = 4 (обез.) — берут и то, и другое.
Ответ: 4 обезьяны.
Задание 2.
123 + 45 — 67 + 8 — 9 = 100; 123 — 4 — 5 — 6 — 7 + 8 — 9 = 100; 123 – 45 — 67 + 89 = 100; 1 +2 + 3 — 4 + 5 + 6 + 78 + 9= 100.
Задание 3.
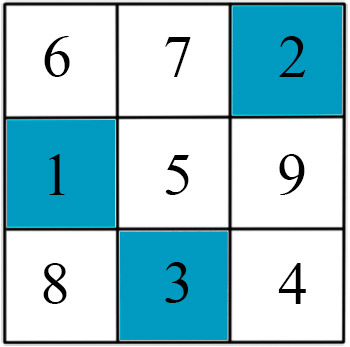
Задание 4.
315 · 41 = (315 · 1) + (315 · 40) = 12915.
Задача 5.
Пусть х — сыр, Зх — мышонок, х + Зх — мышонок и сыр,
4х + 100 — мышь;
4х + 4х + 100 = 180;
8х = 80х = 10. Сыр весит 10 г, мышонок — 30 г, мышь — 140 г.
Задание 6.
44 + 44/4 = 55
IV тур
Задание 1.
Написать 20 при помощи 4-х девяток.
Задача 2.
В клетке находятся фазаны и кролики. У всех животных 35 голов и 94 ноги. Сколько в клетке фазанов и сколько кроликов?
Задача 3.
Червяк ползёт по стволу липы. Ночью он поднимается на 4 м вверх, а днём спускается на 2 м вниз. На восьмую ночь червяк достиг вершины дерева. Как высока липа?
Задание 4.
В записи 8-значного числа используются по 2 раза цифры 1, 2, 3, 4, причём первая цифра — 4. Интересно, что между двумя единицами стоит одна цифра, между двумя двойками — две цифры, между двумя тройками — три цифры, между двумя четвёрками — четыре цифры. Что это за число?
Задача 5.
В коробке лежат десять пар чёрных и столько же пар коричневых перчаток. Сколько перчаток нужно вынуть из коробки не глядя, чтобы быть уверенным, что из них можно будет подобрать хотя бы одну одноцветную пару?
Задача 6.
Кузнецу принесли пять обрывков одной цепи, состоящей из 3, 4, 5, 6 и 7 звеньев, и предложили соединить все обрывки в одну общую цепь. Какое наименьшее число звеньев нужно расковать и снова сковать для выполнения такого заказа?
Ответы
Задание 1.
99/9 + 9 = 20
Задача 2.
12 кроликов и 23 фазана.
Задача 3.
За 7 суток – на (4 — 2) · 7 = 14 (м); 14 + 4 = 18 (м) — высота липы.
Задание 4.
Число 41312432.
Задача 5.
Необходимо вынуть 21 перчатку, так как из вынутых 20 перчаток могут оказаться 10 чёрных и 10 коричневых, и все перчатки будут на одну руку (левую или правую).
Задача 6.
Нужно взять обрывок цепи, состоящий из трёх звеньев, расковать все звенья, соединить ими оставшиеся четыре обрывка и сковать снова три звена.