Сценарий внеклассного мероприятия по математике для учащихся 7 класса «Нить Ариадны»
Ход мероприятия
Ведущий 1. Вы наверняка обратили внимание на необычное название нашего математического праздника. Познакомим наших зрителей с легендой, с которой связано это название. А расскажут ее знатоки древнегреческой мифологии.
Выходят двое участников — «историков», которые попеременно читают легенду.
Когда Тесей пришел в Афины, вся Аттика была погружена в глубокую печаль. С Крита от могущественного царя Миноса прибыли послы за данью. Тяжела и позорна была эта дань. Минос наложил ее на афинян за то, что они убили его сына. Афиняне должны были каждые 9 лет посылать на Крит 7 юношей и 7 девушек. Там они запирались в громадном лабиринте, и их пожирал Минотавр — ужасное чудище с туловищем человека и головой быка.
Тесей решил отправиться с афинскими юношами и девушками на Крит, освободить их и прекратить уплату ужасной дани: вступить в бой с Минотавром не на жизнь, а на смерть. Престарелый Эгей не хотел и слышать об отъезде своего единственного сына, но Тесей настоял на своем.
И вот Тесей отправился на Крит. Корабль благополучно прибыл к острову. Афинских юношей и девушек отвели к Миносу. Могущественный царь Крита сразу обратил внимание на прекрасного юношу. Заметила его и дочь царя Ариадна, а покровительница Тесея Афродита вызвала в сердце Ариадны любовь к юному сыну Эгея. Ариадна решила помочь Тесею, она и думать не могла о том, чтобы юный герой погиб в лабиринте, растерзанный Минотавром. Тайно от отца она дала Тесею острый меч и клубок ниток. Когда Тесея и всех обреченных отвели на растерзание чудовищу в лабиринт, Тесей привязал у его входа конец клубка и пошел по запутанным бесконечным переходам лабиринта, из которого невозможно было найти выход. Постепенно разматывал он клубок, чтобы найти по нити обратный путь. Тесей вступил в схватку с Минотавром, схватил его за рога и вонзил в грудь острый меч. Убив Минотавра, он с помощью нити вышел из лабиринта и вывел всех афинских юношей и девушек. У выхода его встретила Ариадна.
Ведущий. Выражение «нить Ариадны» стало крылатым. В наши дни оно означает способ разрешения проблем; ниточку, ведущую к верному решению; путь, ведущий к цели в сложных условиях.
И вот сегодня каждому из игроков предстоит испытать себя в роли Тесея. В качестве острого меча нужно взять с собой острый ум и найти верный выход из каждой игровой ситуации с целью одержать победу в сегодняшнем состязании. При выполнении заданий каждому предстоит искать свою «нить Ариадны».
Теперь, когда вам стало понятно название нашей игры, приглашаем на сцену 7 юношей и 7 девушек из 7 класса. Съест ли их Минотавр, или они, как Тесей, смогут победить его, пока никому неизвестно. (Выходят участники игры в соответствующих костюмах — поверх одежды из белых простыней надета одежда, напоминающая хитоны древних греков.)
Отправится с ними и Тесей — ученик 9 класса, к которому в самых сложных ситуациях игроки могут обращаться за помощью. Он является вашим научным консультантом, с которым можно посоветоваться не более двух раз за игру.
Минотавр у нас сегодня особенный, математический. Он расставил в разных частях своего лабиринта коварные ловушки, выбраться из которых можно только с помощью знания математики и смекалки.
Вот наши афиняне вошли в лабиринт и дошли до первого перекрестка (ассистенты выносят две арки, на которых укреплены листы с записями). Путей всего два. Но какой из них правильный? И тут становится ясно, что пути помечены математическими записями. На одном написано, что 6 : 2, а на втором – ¼ : ½. Какая из записей правильная? Сделайте свой выбор и идите туда, куда считаете нужным.
Те, кто пошли правильным путем, получают бумажную или тканевую ленту с написанным на ней названием задания, в данном случае «запись». Все полученные в результате игры ленточки связываются друг с другом, образуя «нить Ариадны». Тот, у кого она окажется короче определенной длины, остается в плену у Минотавра, так как не сможет найти обратной дороги (на время выбывает из игры). Игрок с «нитью» наибольшей длины на определенном этапе может выручить одного из пленников по своему усмотрению, ответив на дополнительный вопрос ведущего. Кроме того, в зале (в «лабиринте») находится несколько подсказок. Если игроки смогут найти их, то выберутся из лабиринта не с пустыми руками.
Ведущий. Подходим к следующей развилке. Здесь уже не 2, а целых 3 пути. Они помечены словами: «один», «ни одного» и «множество». А пройти нужно по тому пути, на котором написано количество корней уравнения 3х — 3(х + 8) = 4.
Ведущий 2. И снова те, кто выбрали правильный путь, получают ленточки, но уже со словом «уравнение». А те, кто пошли не туда, вынуждены возвращаться, и, конечно же, их ниточка становится короче, так как отмотали от нее больше.
Ведущий. Подойдя к следующей развилке на расстояние 19 м, наши путники заметили, что за развилкой над каждым проходом через каждую минуту опускается решетка. С какой скоростью нужно двигаться, чтобы успеть преодолеть расстояние в 19 м до решеток?
Варианты ответов (правильный ответ выделен курсивом): 1,2 км/ч, 30 см/с.
Вручаются ленточки со словом «скорость».
Ведущий. Получив ленточки и связав их с предыдущими, игроки продолжают свой путь. Дроби — вот с чем предстоит им справиться на следующей развилке. Это не так-то просто. Ведь недаром у немцев существует поговорка «попасть в дроби», что означает «попасть в затруднительное положение».
Итак, кто правильно сможет вычислить значение выражения, содержащего и обыкновенные, и десятичные дроби, тот узнает правильный путь, — ведь он помечен именно этим числом.
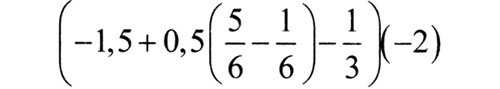
Варианты ответов: 3; -3; 0,2.
Вручаются ленточки со словом «дроби».
Ведущий. Как много зависит от взгляда на какую-то проблему под определенным углом зрения! И если вы хорошо разбираетесь в углах, то никакие проблемы вам не страшны. А задача такова: из двух смежных углов один вдвое больше другого. Какова градусная мера меньшего из них?
Варианты ответов: 30°, 60°, 120°.
Выбравшие правильный путь получают ленточку со словом «углы».
Ведущий. Какая фигура может быть проще отрезка? Наверное, этот тупик наши ребята пройдут быстро. Задача: на отрезке поставили две точки. Сколько отрезков получилось?
Варианты ответов: 3; 4; 6.
Ведущий. А вот и следующая развилка. Но тут кто-то есть. (Выходит ученик с накинутой на голову тканью, закрывающей лицо). Кто ты, милый человек?
Ученик. Не важно, кто я, — важно, зачем я здесь.
Ведущий. И зачем?
Ученик. А затем, чтобы загадывать блуждающим по лабиринту загадки. Правда, редко кто доходит до меня. Я так рад видеть здесь людей, поэтому попрошу вас всего-навсего отгадать число. Его надо будет написать на бумаге. Кто 3 раза справится с моим заданием, того пропущу дальше.
Загадка 1.
Я ни простое, ни составное,
Одновременно доброе и злое.
У натуральных чисел счет я начинаю.
Думаю, все вы меня узнали. (1.)
Загадка 2.
Одновременно я числительное
И глагол — слово повелительное. (3.)
Загадка 3.
В моей записи столько цифр,
Сколько букв мое имя содержит.
А когда рядом станет процент,
Говорят, что сбылись все надежды.
Если мною считают года,
Про меня тут же все забывают,
Для обозначенья меня
Иногда букву «С» применяют. (100.)
Тем, кто правильно написал все числа, ученик вручает ленты со словом «числа».
Ведущий. Вы успешно прошли 7 перекрестков и приблизились к следующей развилке; на ней даже написана цифра 7. А вот и три выражения, значение одного из которых равно 7. (Выходят ассистенты с арками. На их костюмах прикреплена цифра 7, выражения они держат пока «задом наперед», чтобы игроки не видели, что на них написано. Переворачивают их нужной стороной по сигналу ведущего, который засекает время; когда время истекло, разворачивают обратно.) На то, чтобы пройти дальше, дается всего-навсего 7 секунд. Выбрать надо тот путь, который помечен нужным выражением, значение которого равно 7.
Выражения:
1) (6 x 5 + 5) : 5;
2) 40 : 8 + 4;
3) 35 : 7 — 2.
Ведущий. Тот, кто прилагает старание, обязательно добивается успеха, это жизненная аксиома. А хорошо ли знают наши путники аксиомы математические? Три арки, на каждой из которых написаны математические предложения: «сумма смежных углов равна 180°», «через 2 точки можно провести только одну прямую», «вертикальные углы равны». Пойти нужно туда, где написано утверждение, являющееся аксиомой.
Звучат фанфары.
Ведущий. Вот вы и забрались в глубь лабиринта. Где-то здесь рыщет Минотавр. Сравним длины ваших ленточек. Тот, у кого лента состоит менее чем из четырех звеньев, остается в плену у чудовища. А у кого нить самая длинная? Не желает ли этот афинянин выручить товарищей?
«Оставшиеся в плену» выбывают из игры, занимая места в зрительном зале.
Ведущий. А теперь те, кто не попали в плен, займутся поиском подсказок. Напомню, что их всего 5. Для определения их местонахождения необходимо разгадать загадки. В одном из этих предметов вы найдете либо картинку, либо слово, либо вещь. Возможно, отгадка и является подсказкой.
Загадки.
1) Я все знаю, всех учу, но всегда сама молчу.
Ответ: книга. (В одну из книг вложена тканевая лента.)
2) Есть спина, а не лежит никогда.
Есть четыре ноги, а не ходят и три.
Сам всегда стоит,
А всем сидеть велит.
Ответ: стул. (На одном из стульев внизу с помощью скотча приклеена картинка с изображением автомобиля.)
3) Он с тобою и со мною
Шел лесными стежками.
Друг походный за спиною
На ремнях с застежками.
Ответ: рюкзак. (В одном из рюкзаков — листочек, на котором написано: «Памятник Гагарину в Лондоне (2011 г.)».)
4) Это он, это он
Был в арифметику влюблен.
Он назвал ее царицей –
Мир воздал ему сторицей.
Ему присвоили не зря
При жизни титул короля.
Он безупречно вычислял,
Таблицы в памяти держал.
Ответ: Гаусс. (Нужно выбрать его портрет из предложенных портретов математиков.)
5) Два кольца, два конца,
Посередине гвоздик.
Ответ: ножницы. (Ответ к загадке и есть пятая подсказка.)
Ведущий. Итак, все подсказки у вас в руках. Теперь необходимо проникнуть в тайную комнату, которая закрыта на замок. А замочек не простой — с секретом. Он откроется, только если правильно набрать код. Код состоит из 5 цифр.
Первая цифра — число океанов на земном шаре.
Вторая — наименьшее простое число.
Третья — число, не являющееся ни простым, ни составным.
Четвертая — число музыкантов в квинтете.
Пятая — число квадратиков, из которых состоит каждая фигурка в игре «Тетрис».
Если код не будет введен верно через 30 секунд, замок заблокируется, и тогда игроки не смогут попасть в тайную комнату. Время пошло (включает метроном или переворачивает песочные часы).
(Игроки набирают код на блокноте с кодом. Если они не уверены в какой-то цифре, то могут ее подобрать.)
И вот наши отважные афиняне оказываются в секретной комнате, где в сундуках спрятаны богатства царя Миноса. Сундуки одинаковые, но каждый имеет свой секрет. Если выбрать не тот сундук, то все, что в нем находится, при открывании исчезает, испаряется. А в нужном сундуке богатства остаются. Итак, 3 сундука.
(Ассистенты выносят 3 шкатулки с надписями: «Решето Эратосфена», «Круги Эйлера», «Лента Мебиуса». Первые две пустые, в третьей находится лента, полученная путем склеивания бумажной полосы с поворотом на 180°.)
Какой сундук вы выбираете? Прежде чем ответить, внимательно проанализируйте все имеющиеся у вас подсказки.
Итак, что находится в сундуках? (Открывает по очереди каждую из шкатулок.)
В третьем сундуке мы видим поверхность, которая носит название «лента Мебиуса».
Наши выбравшиеся из лабиринта афиняне вместе с Тесеем возвращаются домой (дети садятся на свои места, получив призы в виде игрушки лабиринта), а мы внимательно рассмотрим, что интересного хранилось в сокровищнице (демонстрирует ленту Мебиуса).
Лента Мебиуса относится к числу математических неожиданностей. Говорят, что немецкому профессору Августу Фердинанду Мебиусу, ученику Гаусса, открыть эту поверхность помогла служанка, случайно перекрутив края ленты, которую нужно было склеить. Эта поверхность оказалась очень любопытной. Самым поразительным было то, что у нее всего одна сторона. Чтобы убедиться в этом, проведем небольшой опыт.
(Вызываются два ученика, желающие выполнить опыт. Одному из них дается простое склеенное из бумаги кольцо, второму — лента Мебиуса.)
Начните раскрашивать поверхность с любого места. Что мы видим? У первого ученика поверхность двусторонняя: одна сторона ее оказалась окрашенной, а вторая — нет. А у второго после завершения работы мы обнаруживаем, что вся поверхность оказалась окрашенной, хотя он ни разу не пересекал края ленты, чтобы перейти на другую сторону. Этим и подтверждается односторонность поверхности (ученики возвращаются на свои места).
Действительно, у этой ленты нет ни начала, ни конца. Недаром англичане, чтобы увековечить первого человека, полетевшего в космос, в честь 50-летия этого события (в 2011 г.) расположили памятник Юрию Гагарину так, что он как бы шагает в бесконечность именно по ленте Мебиуса.
Это свойство ленты с успехом было использовано в технике. Если у ременной передачи ремень сделан в виде ленты Мебиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца, что дает ощутимую экономию. А вот и настоящий ремень передач, который используется в автомобиле (показывает).
Другие неожиданности подстерегают нас, если мы используем ножницы. Кто желает исполнить роль фокусника? (Вызывается желающий.) Тот зритель, который сможет угадать, что произойдет, если мы разрежем ленту вдоль посередине, получит ленту Мебиуса в подарок для дальнейших экспериментов. Высказывайте свои предположения.
Действуй, фокусник (ученик разрезает ленту)! Что мы видим? Обычное кольцо распалось бы при этом на два куска, а лента превратилось в одно перекрученное кольцо. Еще удивительнее, что это кольцо оказывается двусторонним.
А если разрезать так, чтобы линия разреза проходила в два раза ближе к левому краю ленты, чем к правому, что-нибудь изменится? (Получается два сцепленных между собой кольца разного размера.)
Теперь возьмем ленту, которую, прежде чем склеить, перекрутили не на 180°, а на 360°. Эта поверхность уже двусторонняя, но свойства у нее не менее интересные. Разрежем ее, как и первую, вдоль посередине. Что получится? Попробуйте догадаться. (2 кольца, сцепленных между собой.) А теперь разрежем каждое из этих колец посередине вдоль. Сколько колец должно получиться? (3.)
Вот какую интересную забаву привезли нам игроки из лабиринта.
А мы заканчиваем нашу игру такими замечательными словами:
Каков бы ни был лабиринт,
Мы выйти из него сумеем,
Ведь логика и интеллект
Все открывают в жизни двери.
А этот дар, дар размышлять,
Он человеку дан не зря ведь,
Должны его тренировать,
Задачи разные решая.
Вы с математикой дружите:
Она подскажет верный путь,
Научит, как, идя по жизни,
С пути ни разу не свернуть.



 Внеклассное мероприятие по математике 7 класс к неделе математики
Внеклассное мероприятие по математике 7 класс к неделе математики